
【题目】双曲线![]() 经过点
经过点![]() ,两条渐近线的夹角为
,两条渐近线的夹角为![]() ,直线
,直线![]() 交双曲线于
交双曲线于![]() 、
、![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若![]() 过原点,
过原点,![]() 为双曲线上异于
为双曲线上异于![]() 、
、![]() 的一点,且直线
的一点,且直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 过双曲线的右焦点
过双曲线的右焦点![]() ,是否存在
,是否存在![]() 轴上的点
轴上的点![]() ,使得直线
,使得直线![]() 绕点
绕点![]() 无论怎样转动,都有
无论怎样转动,都有![]() 成立?若存在,求出
成立?若存在,求出![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]()
(2)证明见解析
(3)存在,![]() .
.
【解析】
(1)根据双曲线所过的点和渐近线的夹角可得关于![]() 的方程组,解该方程组后可得双曲线的标准方程.
的方程组,解该方程组后可得双曲线的标准方程.
(2)设![]() ,
,![]() ,
,![]() ,用三点的坐标表示
,用三点的坐标表示![]() ,再利用点满足的方程化简前者可得所求的定值.
,再利用点满足的方程化简前者可得所求的定值.
(3)设直线![]() 为
为![]() ,
,![]() ,
,![]() ,根据
,根据![]() 可得恒等式
可得恒等式![]() ,联立直线方程和双曲线方程后利用韦达定理化简前者可得
,联立直线方程和双曲线方程后利用韦达定理化简前者可得![]() ,从而得到所求的定点.
,从而得到所求的定点.
(1)双曲线的渐近线方程为![]() ,
,
因为两条渐近线的夹角为![]() ,故渐近线
,故渐近线![]() 的倾斜角为
的倾斜角为![]() 或
或![]() ,
,
所以![]() 或
或![]() .
.
又![]() ,故
,故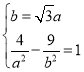 或
或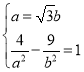 (无解),故
(无解),故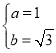 ,
,
所以双曲线![]() .
.
(2)设![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 即
即![]() ,
,
所以![]() 为定值
为定值![]() .
.
(3)双曲线的右焦点为![]() ,
,
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]() ,设
,设![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
整理得到![]() ①,
①,
由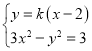 可以得到
可以得到![]() ,
,
因为直线![]() 与双曲线有两个不同的交点,
与双曲线有两个不同的交点,
故![]() 且
且![]() ,
,
所以![]() .
.
由题设有①对任意的![]() 总成立,
总成立,
因![]() ,
,
所以①可转化为![]() ,
,
整理得到![]() 对任意的
对任意的![]() 总成立,
总成立,
故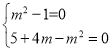 ,故
,故![]() 即所求的定点
即所求的定点![]() 的坐标为
的坐标为![]() .
.
当直线![]() 的斜率不存在时,则
的斜率不存在时,则![]() ,此时
,此时![]() 或
或![]() ,
,
此时![]() .
.
综上,定点![]() 的坐标为
的坐标为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知直线y=2x﹣m与抛物线C:y2=2px(p>0)交于点A,B.
(1)m=p且|AB|=5,求抛物线C的方程;
(2)若m=4p,求证:OA⊥OB(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
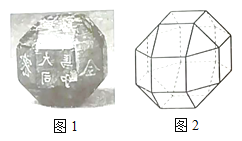
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和为
的前n项和为![]() ,并且
,并且![]() ,数列
,数列![]() 满足:
满足:![]() ,
,![]() ,记数列
,记数列![]() 的前n项和为
的前n项和为![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 及前n项和为
及前n项和为![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() 及前n项和为
及前n项和为![]() ;
;
(3)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为手机作为华为公司三大核心业务之一,2018年的销售量跃居全球第二名,某机构随机选取了100名华为手机的顾客进行调查,并将这![]() 人的手机价格按照
人的手机价格按照![]() ,
,![]() ,…
,…![]() 分成
分成![]() 组,制成如图所示的频率分布直方图,其中
组,制成如图所示的频率分布直方图,其中![]() 是
是![]() 的
的![]() 倍.
倍.

(1)求![]() ,
,![]() 的值;
的值;
(2)求这![]() 名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
(3)利用分层抽样的方式从手机价格在![]() 和
和![]() 的顾客中选取
的顾客中选取![]() 人,并从这
人,并从这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求抽取的
人进行回访,求抽取的![]() 人手机价格在不同区间的概率.
人手机价格在不同区间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com