
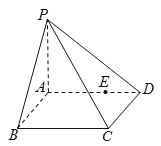
【题目】如图,四棱锥![]() 中,
中,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,四棱锥外接球的球心为
,四棱锥外接球的球心为![]() ,点
,点![]() 是棱
是棱![]() 上的一个动点.给出如下命题:①直线
上的一个动点.给出如下命题:①直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;②![]() 与
与![]() 一定不垂直;③三棱锥
一定不垂直;③三棱锥![]() 的体积为定值;④
的体积为定值;④![]() 的最小值为
的最小值为![]() .其中正确命题的序号是______________.(将你认为正确的命题序号都填上)
.其中正确命题的序号是______________.(将你认为正确的命题序号都填上)
【答案】①③④
【解析】
由题意画出图形,由异面直线的概念判断①;利用线面垂直的判定与性质判断②;找出球心,由棱锥底面积与高为定值判断③;设![]() ,列出
,列出![]() 关于
关于![]() 的函数式,结合其几何意义求出最小值判断④.
的函数式,结合其几何意义求出最小值判断④.
解:对于①,![]() 直线
直线![]() 经过平面
经过平面![]() 内的点
内的点![]() ,而直线
,而直线![]() 在平面
在平面![]() 内不过
内不过![]() ,
,![]() 直线
直线![]() 与直线
与直线![]() 是异面直线,故①正确;
是异面直线,故①正确;
对于②,当![]() 与
与![]() 重合时,
重合时,![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() 垂直
垂直![]() ,故②错误;
,故②错误;
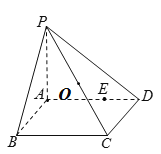
对于③,由题意知,四棱锥![]() 的外接球的球心为
的外接球的球心为![]() 是
是![]() 的中点,则△
的中点,则△![]() 的面积为定值,且
的面积为定值,且![]() 到平面
到平面![]() 的距离为定值,
的距离为定值,![]() 三棱锥
三棱锥![]() 的体积为定值,故③正确;
的体积为定值,故③正确;
对于④,设![]() ,则
,则![]() ,
,![]() .
.
由其几何意义,即平面内动点![]() 与两定点
与两定点![]() ,
,![]() 距离和的最小值知,其最小值为
距离和的最小值知,其最小值为![]() ,故④正确.
,故④正确.
故答案为:①③④.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
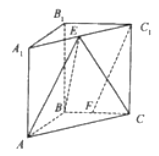
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
, ![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 交椭圆
交椭圆![]() 于另一个点
于另一个点![]() ,求
,求![]() 面积取得最大值时直线
面积取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为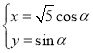 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时
的最小值及此时![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com