
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见证明;(2)![]()
【解析】
(1) 设F(x)=e2x+ln(x+1)﹣(x+1)2﹣x(x≥0),通过两次求导,判断F(x)的单调性,即可得证;(2) 由题意可得存在x0∈[0,+∞),使得e![]() ﹣ln(x0+a)﹣x02<0,设
﹣ln(x0+a)﹣x02<0,设![]() =e2x﹣ln(x+a)﹣x2,两次求导,判断单调性,对a讨论,分①当a≥
=e2x﹣ln(x+a)﹣x2,两次求导,判断单调性,对a讨论,分①当a≥![]() 时,②当a<
时,②当a<![]() 时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
(1)设![]() ,
,![]()
F″(x)=4e2x﹣![]() ﹣2=[e2x-
﹣2=[e2x-![]() ]+2(e2x﹣1)+e2x>0,(x≥0),
]+2(e2x﹣1)+e2x>0,(x≥0),
所以,F′(x)在[0,+∞)上递增,所以F′(x)≥F′(0)=0,
所以,F(x)在[0,+∞)上递增,所以F(x)≥F(0)=0,
即有当x≥0时,f(x)≥(x+1)2+x;
(2)即![]() ,
,
则![]() ,
,![]()
![]() 在
在![]() 上递增,
上递增,![]()
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
故![]() ,
,![]()
②当![]() 时,
时,![]()
设![]() ,
,
![]() ,
,
![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
![]() ,
,
![]() ,
,
则当![]() 时,
时,![]() 恒成立,不合题意
恒成立,不合题意
综上,则![]()


科目:高中数学 来源: 题型:
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量×(万辆) | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度(微克/立方米) | 60 | 70 | 74 | 78 | 79 |
(1)根据上表数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)若周六同一时间段的车流量是25万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度为多少(保留整数)?
参考公式:由最小二乘法所得回归直线的方程是:![]() ,其中
,其中 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验将![]() 只小鼠随机分成
只小鼠随机分成![]() 、
、![]() 两组,每组
两组,每组![]() 只,其中
只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比根据试验数据分别得到如图所示的直方图:
组小鼠给服乙离子溶液每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比根据试验数据分别得到如图所示的直方图:


根据频率分布直方图估计,事件![]() :“乙离子残留在体内的百分比不高于
:“乙离子残留在体内的百分比不高于![]() ”发生的概率
”发生的概率![]() .
.
(1)根据所给的频率分布直方图估计各段频数;
(附:频数分布表)
|
|
|
|
|
|
| |
|
|
| |
|
|
|
|
|
|
| |
|
|
| |
(2)请估计甲离子残留百分比的中位数,请估计乙离子残留百分比的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中x的值;
(2)如果上学所需时间不少于1小时的学生可申请在学校住宿,若该学校有600名新生,请估计新生中有多少名学生可以申请住宿;
(3)由频率分布直方图估计该校新生上学所需时间的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
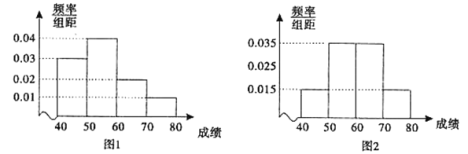
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com