Question

【题目】已知是定义在R上的奇函数，且当时，.

（1）求函数的解析式；

（2）当时，不等式恒成立，求实数a的取值范围.

Answer 1

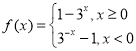【答案】（1）；（2）

【解析】

（1）根据奇函数的性质即可求出；

（2）根据函数的单调性和奇函数的性质可得不等式f（log22x）+f（5-alog2x）≥0恒成立，t=log2x，问题转化为对t∈[2，5]恒成立，分离参数，根据导数求最值即可求出a的取值范围．

（1）由题意可知：是定义在上的奇函数，

，

当，，代入可得，

即，

当时，，

，

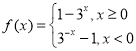综上所述，结论：函数的解析式；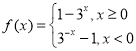

（2）由题意可知：，

化解得：，

又是定义在上的奇函数，

∴，

令，，，则原不等式变为，

∵，

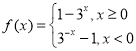求导可知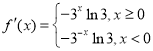，在上恒成立，

故在上单调递减，

，化简得，在上恒成立，

，

设，，

令，解得，则函数在上单调递增，

令，解得，则函数在上单调递减，

，，，则，

，

综上所述，结论：的取值范围是.