
【题目】已知函数![]() .
.
(1)若![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)由![]() 得
得![]() ,根据
,根据![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,则
,则![]() 有两个不同的零点,即方程
有两个不同的零点,即方程![]() 有两个不同的实根,转化为直线
有两个不同的实根,转化为直线![]() 与
与![]() 的图象有两个不同的交点求解.
的图象有两个不同的交点求解.
(2)由(1)知![]() ,设
,设![]() ,则
,则![]() ,由
,由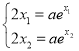 得
得![]() ,
,![]() ,要证
,要证![]() ,将
,将![]() 代入整理为
代入整理为![]() ,再令
,再令![]() ,转化为
,转化为![]() ,再构造函数
,再构造函数![]() ,研究其最大值即可.
,研究其最大值即可.
(1)由![]() 得
得![]() ,
,
![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,则
,则![]() 有两个不同的零点,
有两个不同的零点,
即方程![]() 有两个不同的实根,
有两个不同的实根,
即直线![]() 与
与![]() 的图象有两个不同的交点,
的图象有两个不同的交点,
设![]() ,则
,则![]() ,
,
![]() 时
时![]() ,
,![]() 单调递增,且
单调递增,且![]() 的取值范围是
的取值范围是![]() ;
;
![]() 时
时![]() ,
,![]() 单调递减,且
单调递减,且![]() 的取值范围是
的取值范围是![]() ,
,
所以当![]() 时,直线
时,直线![]() 与
与![]() 的图象有两个不同的交点,
的图象有两个不同的交点,
![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)知![]() ,设
,设![]() ,则
,则![]() ,
,
由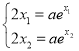 得
得![]() ,
,![]()
所以要证![]() ,只需证
,只需证![]() ,
,
即证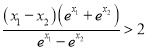 ,即证
,即证![]() ,
,
设![]() ,即证
,即证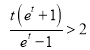 ,即证
,即证![]() ,
,
设![]() ,则
,则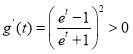 ,
,
所以![]() 在
在![]() 是增函数,
是增函数,![]() ,
,
所以![]() ,从而有
,从而有![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】由甲、乙、丙三个人组成的团队参加某项闯关游戏,第一关解密码锁,3个人依次进行,每人必须在1分钟内完成,否则派下一个人.3个人中只要有一人能解开密码锁,则该团队进入下一关,否则淘汰出局.根据以往100次的测试,分别获得甲、乙解开密码锁所需时间的频率分布直方图.
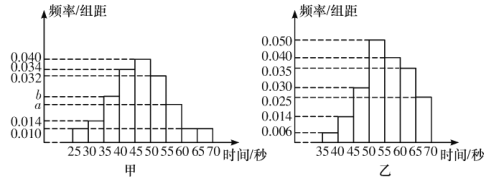
(1)若甲解开密码锁所需时间的中位数为47,求![]() 、
、![]() 的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
(2)若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率,并且丙在1分钟内解开密码锁的概率为0.5,各人是否解开密码锁相互独立.
①按乙丙甲的先后顺序和按丙乙甲的先后顺序哪一种可使派出人员数目的数学期望更小.
②试猜想:该团队以怎样的先后顺序派出人员,可使所需派出的人员数目![]() 的数学期望达到最小,不需要说明理由.
的数学期望达到最小,不需要说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
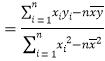 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为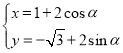 (其中
(其中![]() 为参数,
为参数,![]() ).在极坐标系(以坐标原点
).在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,曲线
轴非负半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 上恰有一个点到曲线
上恰有一个点到曲线![]() 的距离为1,求曲线
的距离为1,求曲线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)若数列![]() 的首项为
的首项为![]() ,其中
,其中![]() ,且
,且![]() ,
,![]() ,
,![]() 构成公比小于0的等比数列,求
构成公比小于0的等比数列,求![]() 的值;
的值;
(2)若![]() 是公差为d(d>0)的等差数列
是公差为d(d>0)的等差数列![]() 的前n项和,求
的前n项和,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,且数列
,且数列![]() 单调递增,数列
单调递增,数列![]() 单调递减,求数列
单调递减,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()

(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
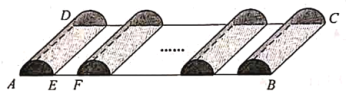
【题目】如图,某人承包了一块矩形土地![]() 用来种植草莓,其中
用来种植草莓,其中![]() m,
m,![]() m.现规划建造如图所示的半圆柱型塑料薄膜大棚
m.现规划建造如图所示的半圆柱型塑料薄膜大棚![]() 个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米
个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米![]() 元;另外,还需在每个大棚之间留下
元;另外,还需在每个大棚之间留下![]() m宽的空地用于建造排水沟与行走小路(如图中
m宽的空地用于建造排水沟与行走小路(如图中![]() m),这部分建设造价为每平方米
m),这部分建设造价为每平方米![]() 元.
元.
(1)当![]() 时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留
时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留![]() )
)
(2)试确定大棚的个数,使得上述两项费用的和最低?(本小题计算中![]() 取
取![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com