
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 的直线与椭圆交于
的直线与椭圆交于![]() 的两点,且
的两点,且![]() 轴,若
轴,若![]() 为椭圆上异于
为椭圆上异于![]() 的动点且
的动点且![]() ,则该椭圆的离心率为___.
,则该椭圆的离心率为___.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】下列叙述中正确的个数是( )
①将一组样本数据中的每个数据都加上同一个常数后,方差不变;
②命题![]() ,
,![]() ,命题
,命题![]() ,
,![]() ,则
,则![]() 为真命题;
为真命题;
③“![]() ”是“
”是“![]() 的必要而不充分条件;
的必要而不充分条件;
④将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象.
的图象.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学家到乙同学家的途中有一座公园,甲同学家到公园的距离与乙同学家到公园的距离都是2km.如图所示表示甲同学从家出发到乙同学家经过的路程y(km)与时间x(min)的关系,下列结论正确的是( )
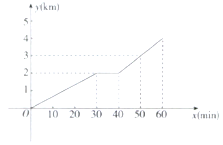
A.甲同学从家出发到乙同学家走了60min
B.甲从家到公园的时间是30min
C.甲从家到公园的速度比从公园到乙同学家的速度快
D.当![]() 时,y与x的关系式为
时,y与x的关系式为![]()
E.当![]() 时,y与x的关系式为
时,y与x的关系式为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某球员是当今![]() 国内最好的球员之一,在
国内最好的球员之一,在![]() 赛季常规赛中,场均得分达
赛季常规赛中,场均得分达![]() 分。
分。![]() 分球和
分球和![]() 分球命中率分别为
分球命中率分别为![]() 和
和![]() ,罚球命中率为
,罚球命中率为![]() .一场
.一场![]() 比赛分为一、二、三、四节,在某场比赛中该球员每节出手投
比赛分为一、二、三、四节,在某场比赛中该球员每节出手投![]() 分的次数分别是
分的次数分别是![]() ,
,![]() ,
,![]() ,
,![]() ,每节出手投三分的次数分别是
,每节出手投三分的次数分别是![]() ,
,![]() ,
,![]() ,
,![]() ,罚球次数分别是
,罚球次数分别是![]() ,
,![]() ,
,![]() ,
,![]() (罚球一次命中记
(罚球一次命中记![]() 分)。
分)。
(1)估计该球员在这场比赛中的得分(精确到整数);
(2)求该球员这场比赛四节都能投中三分球的概率;
(3)设该球员这场比赛中最后一节的得分为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快,已知每投放![]() 个(
个(![]() ,且
,且![]() )单位的洗衣液在一定量水的洗衣机中, 它在水中释放的浓度
)单位的洗衣液在一定量水的洗衣机中, 它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中 .若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液浓度不低于
.若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液浓度不低于![]() 克/升时,它才能起到有效去污的作用.
克/升时,它才能起到有效去污的作用.
(1)若只投放一次![]() 个单位的洗衣液,当两分钟时水中洗衣液的浓度为
个单位的洗衣液,当两分钟时水中洗衣液的浓度为![]() 克/升,求
克/升,求![]() 的值;
的值;
(2)若只投放一次![]() 个单位的洗衣液,则有效去污时间可达几分钟?
个单位的洗衣液,则有效去污时间可达几分钟?
(3)若第一次投放![]() 个单位的洗衣液,
个单位的洗衣液,![]() 分钟后再投放
分钟后再投放![]() 个单位的洗衣液,则在第
个单位的洗衣液,则在第![]() 分钟时洗衣液是否还能起到有效去污的作用?请说明理由.
分钟时洗衣液是否还能起到有效去污的作用?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com