
 ,已知S的身高约为
,已知S的身高约为 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按 米处理)
米处理)
 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.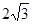 米. (2) 摄影者可以将彩杆全部摄入画面.
米. (2) 摄影者可以将彩杆全部摄入画面.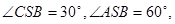
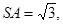 故在
故在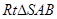 中,可求得BA=3,即摄影者到立柱的水平距离为3米……… 3分
中,可求得BA=3,即摄影者到立柱的水平距离为3米……… 3分 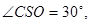 在
在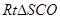 中,可求得
中,可求得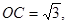
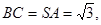 故
故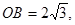 即立柱高为
即立柱高为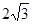 米. -------------- 6分
米. -------------- 6分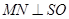 时,
时,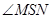 最大,并且此时
最大,并且此时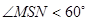 ,得2分)
,得2分)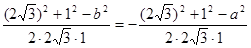
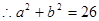 ……8分
……8分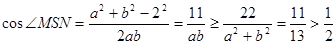


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:不详 题型:解答题
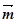 ="(1,cosA" -1),
="(1,cosA" -1),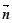 =(cosA,1)且满足
=(cosA,1)且满足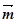 ⊥
⊥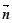 .
. 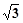 ,b+c=3 求b、c的值.
,b+c=3 求b、c的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com