
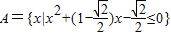 ,
,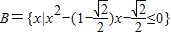 ,又设函数f(x)=2x2+mx-1.
,又设函数f(x)=2x2+mx-1.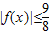 .
. ,故得解;
,故得解; ,由于对任意x∈R,有f(1-x)=f(1+x)成立,可知函数的对称轴为x=1,从而可确定函数f(x)=2x2-4x-1=2(x-1)2-3.,进而可求函数f(x)的值域.
,由于对任意x∈R,有f(1-x)=f(1+x)成立,可知函数的对称轴为x=1,从而可确定函数f(x)=2x2-4x-1=2(x-1)2-3.,进而可求函数f(x)的值域. ,从而f(x)的最小值为-1,最大值在端点处取得,故可证.
,从而f(x)的最小值为-1,最大值在端点处取得,故可证. ,
,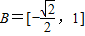
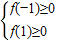
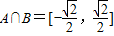
 .
.





 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
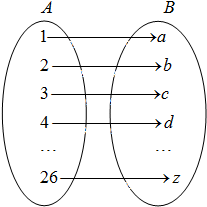 设f是由集合A={x|x∈N,且1≤x≤26}到B={a,b,c,…,z}(即26个英文字母按照字母表顺序排列)的映射,集合B中的任何一个元素在A中也只有唯一的元素与之对应,其对应法则如图所示(依次对齐);又知函数g(x)=
设f是由集合A={x|x∈N,且1≤x≤26}到B={a,b,c,…,z}(即26个英文字母按照字母表顺序排列)的映射,集合B中的任何一个元素在A中也只有唯一的元素与之对应,其对应法则如图所示(依次对齐);又知函数g(x)=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 9 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
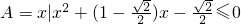 ,
,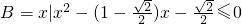 ,又设函数f(x)=2x2+mx-1.
,又设函数f(x)=2x2+mx-1.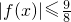 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com