
【题目】已知全集![]()
(1)若![]() ,求实数q的取值范围;
,求实数q的取值范围;
(2)若![]() 中有四个元素,求
中有四个元素,求![]() 和q的值.
和q的值.
【答案】(1)![]() ;
;
(2)![]() ,
, ![]() ={1,3,4,5}
={1,3,4,5}
【解析】试题分析:(1)若![]() =U,则A=
=U,则A=![]() ,根据一元二次方程根的关系即可求q的取值范围;
,根据一元二次方程根的关系即可求q的取值范围;
(2)若![]() 中有四个元素,则等价为A为单元素集合,然后进行求解即可.
中有四个元素,则等价为A为单元素集合,然后进行求解即可.
试题解析:
(1)∵![]() A=U,
A=U,
∴A=![]() ,即方程x2﹣5qx+4=0无解,或方程x2﹣5qx+4=0的解不在U中.
,即方程x2﹣5qx+4=0无解,或方程x2﹣5qx+4=0的解不在U中.
∴△=25q2﹣16<0,∴![]() <q<
<q<![]() ,
,
若方程x2﹣5qx+4=0的解不在U中,
此时满足判别式△=25q2﹣16≥0,即p≥![]() 或p≤﹣
或p≤﹣![]() ,
,
由12﹣5q1+4≠0得q≠1;
由22﹣5q2+4≠0得q≠![]() ;
;
同理,由3、4、5不是方程的根,依次可得q≠![]() ,q≠1,q≠
,q≠1,q≠![]() ;
;
综上可得所求范围是{q|q∈R,且q≠![]() ,q≠1,q≠
,q≠1,q≠![]() }.
}.
(2)∵![]() A中有四个元素,∴A为单元素集合,则△=25q2﹣16=0,
A中有四个元素,∴A为单元素集合,则△=25q2﹣16=0,
即q=±![]() ,
,
当A={1}时,q=1,不满足条件.;
当A={2}时,q=![]() ,满足条件.;
,满足条件.;
当A={3}时,q=![]() ,不满足条件.;
,不满足条件.;
当A={4}时,q=1,不满足条件.;
当A={5}时,q=![]() ,不满足条件.,
,不满足条件.,
∴q=![]() ,此时A={2},
,此时A={2},
对应的UA={1,3,4,5}.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过坐标原点,其到函数为
的图像经过坐标原点,其到函数为![]() ,数列的前
,数列的前![]() 项和为
项和为![]() ,点
,点![]()
![]() 均在函数
均在函数![]() 的图像上.
的图像上.
(I)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() n项和,求使得
n项和,求使得![]() <
<![]() 对所有都成立的最小正整数m.
对所有都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间![]() 上的函数
上的函数![]() ,其中常数
,其中常数![]() .
.
(1)若函数![]() 分别在区间
分别在区间![]() 上单调,试求
上单调,试求![]() 的取值范围;
的取值范围;
(2)当![]() 时,方程
时,方程![]() 有四个不相等的实根
有四个不相等的实根![]() .
.
①证明: ![]() ;
;
②是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 单调,且
单调,且![]() 的取值范围为
的取值范围为![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把1、2、3、4、5这五个数字组成无重复数字的五位数,并把它们由小大到的顺序排成一个数列.
(Ⅰ)求![]() 是这个数列的第几项;
是这个数列的第几项;
(Ⅱ)求这个数列的第96项;
(Ⅲ)求这个数列的所有项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知椭圆方程为![]() ,点
,点![]() .
.
i.若关于原点对称的两点![]() 记直线
记直线![]() 的斜率分别为
的斜率分别为![]() ,试计算
,试计算![]() 的值;
的值;
ii.若关于原点对称的两点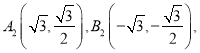 记直线
记直线![]() 的斜率分别为
的斜率分别为![]() ,试计算
,试计算![]() 的值;
的值;
(2)根据上题结论探究:若![]() 是椭圆
是椭圆![]() 上关于原点对称的两点,点
上关于原点对称的两点,点![]() 是椭圆上任意一点,且直线
是椭圆上任意一点,且直线![]() 的斜率都存在,并分别记为
的斜率都存在,并分别记为![]() ,试猜想
,试猜想![]() 的值,并加以证明.
的值,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com