
①AC⊥β;
②AC与α、β所成的角相等;
③AC与CD在β内的射影在同一条直线上;
④AC∥EF.

那么上述几个条件中能成为增加条件的是___________(填上你认为正确的所有答案序号).
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
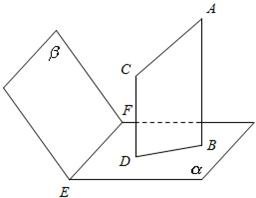 8、如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别为B,D,且AB≠CD.如果增加一个条件就能推出BD⊥EF,给出四个条件:①AC⊥β;②AC⊥EF;③AC与BD在β内的正投影在同一条直线上;④AC与BD在平面β内的正投影所在的直线交于一点.那么这个条件不可能是( )
8、如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别为B,D,且AB≠CD.如果增加一个条件就能推出BD⊥EF,给出四个条件:①AC⊥β;②AC⊥EF;③AC与BD在β内的正投影在同一条直线上;④AC与BD在平面β内的正投影所在的直线交于一点.那么这个条件不可能是( )查看答案和解析>>
科目:高中数学 来源: 题型:
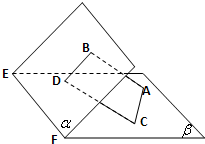 15、如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别为B,D,若增加一个条件,就能推出BD⊥EF,现有:①AC⊥β;②AC与α,β所成的角相等;③AC与CD在β内的射影在同一条直线上;④AC∥EF,那么上述几个条件中能成为增加的条件的序号是
15、如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别为B,D,若增加一个条件,就能推出BD⊥EF,现有:①AC⊥β;②AC与α,β所成的角相等;③AC与CD在β内的射影在同一条直线上;④AC∥EF,那么上述几个条件中能成为增加的条件的序号是查看答案和解析>>
科目:高中数学 来源: 题型:
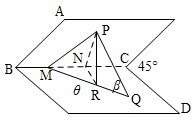 如图,设平面AC和BD相交于BC,它们所成的一个二面角为45°,P为平面AC内的一点,Q为面BD内的一点,已知直线MQ是直线PQ在平面BD内的射影,并且M在BC上又设PQ与平面BD所成的角为β,∠CMQ=θ(0°<θ<90°),线段PM的长为a,求线段PQ的长.
如图,设平面AC和BD相交于BC,它们所成的一个二面角为45°,P为平面AC内的一点,Q为面BD内的一点,已知直线MQ是直线PQ在平面BD内的射影,并且M在BC上又设PQ与平面BD所成的角为β,∠CMQ=θ(0°<θ<90°),线段PM的长为a,求线段PQ的长.查看答案和解析>>
科目:高中数学 来源: 题型:
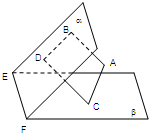 (2009•中山模拟)如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足.分别为B,D,若增加一个条件,就能推出BD⊥EF.现有①AC⊥β;②AC与α,β所成的角相等;③AC与CD在β内的射影在同一条直线上;④AC∥EF.那么上述几个条件中能成为增加条件的个数是( )
(2009•中山模拟)如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足.分别为B,D,若增加一个条件,就能推出BD⊥EF.现有①AC⊥β;②AC与α,β所成的角相等;③AC与CD在β内的射影在同一条直线上;④AC∥EF.那么上述几个条件中能成为增加条件的个数是( )查看答案和解析>>
科目:高中数学 来源: 题型:
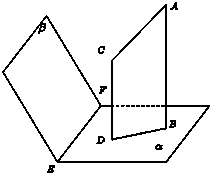 如图,设平面α∩β=EFAB⊥α,CD⊥α垂足分别为B,D,且AB≠CD.如果增加一个条件就能推出BD⊥EF,给出四个条件:
如图,设平面α∩β=EFAB⊥α,CD⊥α垂足分别为B,D,且AB≠CD.如果增加一个条件就能推出BD⊥EF,给出四个条件:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com