
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴为正半轴为极轴建立极坐标系.已知曲线
轴为正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 过定点
过定点![]() 且倾斜角为
且倾斜角为![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)把曲线![]() 化成直角坐标方程,并求
化成直角坐标方程,并求![]() 的值;
的值;
(2)若![]() 成等比数列,求直线
成等比数列,求直线![]() 的倾斜角
的倾斜角![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,曲线C由部分椭圆C1:![]() +
+![]() =1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为![]() .
.

(1)求a,b的值;
(2)过点B的直线l与C1,C2分别交于点P,Q(P,Q,A,B中任意两点均不重合),若AP⊥AQ,求直线l
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
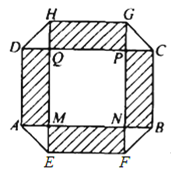
【题目】如图,居民小区要建一座八边形的休闲场所,它的主体造型平面图是由两个相同的矩形![]() 和
和![]() 构成的面积为
构成的面积为![]() 的十字形地域,计划在正方形
的十字形地域,计划在正方形![]() 上建一座花坛,造价为
上建一座花坛,造价为![]() 元/
元/![]() ;在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价为
;在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价为![]() 元/
元/![]() ;再在四个空角(图中四个三角形,如
;再在四个空角(图中四个三角形,如![]() )上铺草坪,造价为
)上铺草坪,造价为![]() 元/
元/![]()
(1)设总造价为![]() (单位:元),
(单位:元),![]() 长为
长为![]() (单位:
(单位:![]() ),试求出
),试求出![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)当![]() 长
长![]() 取何值时,总造价
取何值时,总造价![]() 最小,并求出这个最小值.
最小,并求出这个最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程为:![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,射线l的极坐标方程为
,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,射线l的极坐标方程为![]() ,
,![]() .
.
![]() 将圆C的参数方程化为极坐标方程;
将圆C的参数方程化为极坐标方程;
![]() 设点A的直角坐标为
设点A的直角坐标为![]() ,射线l与圆C交于点
,射线l与圆C交于点![]() 不同于点
不同于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C:![]() 1(a>0,b>0)的左右焦点为F1,F2(|F1F2|=2c),以坐标原点O为圆心,以c为半径作圆A,圆A与双曲线C的一个交点为P,若三角形F1PF2的面积为a2,则C的离心率为_____.
1(a>0,b>0)的左右焦点为F1,F2(|F1F2|=2c),以坐标原点O为圆心,以c为半径作圆A,圆A与双曲线C的一个交点为P,若三角形F1PF2的面积为a2,则C的离心率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]()
![]() 的焦距为
的焦距为![]() ,短半轴的长为2,过点P(-2,1)且斜率为1的直线l与椭圆C交于A,B两点.
,短半轴的长为2,过点P(-2,1)且斜率为1的直线l与椭圆C交于A,B两点.
(1)求椭圆C的方程;
(2)求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元;未售出的产品,每盒亏损30元![]() 根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了160盒该产品,以
根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了160盒该产品,以![]() 单位:盒,
单位:盒,![]() 表示这个开学季内的市场需求量,
表示这个开学季内的市场需求量,![]() 单位:元
单位:元![]() 表示这个开学季内经销该产品的利润
表示这个开学季内经销该产品的利润
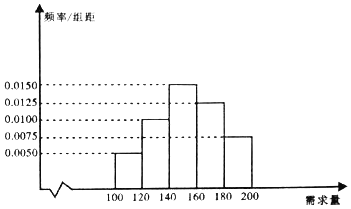
![]() 根据直方图估计这个开学季内市场需求量x的平均数和众数;
根据直方图估计这个开学季内市场需求量x的平均数和众数;
![]() 将y表示为x的函数;
将y表示为x的函数;
![]() 根据直方图估计利润不少于4800元的概率.
根据直方图估计利润不少于4800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设一元二次方程Ax2+Bx+C=0,根据下列条件分别求解:
(1)若A=1,B、C是1枚骰子先后掷两次出现的点数,求方程有实数根的概率;
(2)若B=-A,C=A-3,且方程有实数根,求方程至少有一个非正实数根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com