
【题目】某经销商从沿海城市水产养殖厂购进一批某海鱼,随机抽取50条作为样本进行统计,按海鱼重量(克)得到如图的频率分布直方图:
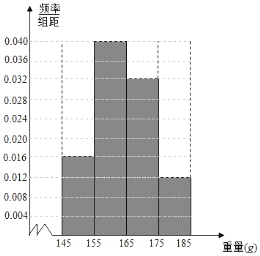
(1)若经销商购进这批海鱼100千克,试估计这批海鱼有多少条(同一组中的数据用该区间的中点值作代表);
(2)根据市场行情,该海鱼按重量可分为三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) |
|
|
|
若经销商以这50条海鱼的样本数据来估计这批海鱼的总体数据,视频率为概率.现从这批海鱼中随机抽取3条,记抽到二等品的条数为X,求x的分布列和数学期望.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在极坐标系中,O为极点,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与
且与![]() 垂直,垂足为P.
垂直,垂足为P.
(1)当![]() 时,求
时,求![]() 及l的极坐标方程;
及l的极坐标方程;
(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 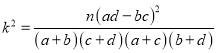 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半圆![]() 的直径的两端点为
的直径的两端点为![]() ,点
,点![]() 在半圆
在半圆![]() 及直径
及直径![]() 上运动,若将点
上运动,若将点![]() 的纵坐标伸长到原来的2倍(横坐标不变)得到点
的纵坐标伸长到原来的2倍(横坐标不变)得到点![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若称封闭曲线上任意两点距离的最大值为该曲线的“直径”,求曲线![]() 的“直径”.
的“直径”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 长度的最大值为4.
长度的最大值为4.
(1)求![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,当直线
,当直线![]() 变化(
变化(![]() 不与
不与![]() 轴重合)时,若
轴重合)时,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com