
【题目】在平面直角坐标系xOy中,D是到原点的距离不大于1的点构成的区域,E是满足不等式组  的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】某工厂第一季度某产品月生产量分别为10万件,12万件,13万件,为了预测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量y (单位:万件)与月份x 的关系.模拟函数1:y=ax+ ![]() +c
+c
;模拟函数2:y=mnx+s.
(1)已知4月份的产量为13.7 万件,问选用哪个函数作为模拟函数好?
(2)受工厂设备的影响,全年的每月产量都不超过15万件,请选用合适的模拟函数预测6月份的产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() )的值域为R;命题q:3x﹣9x<a对一切实数x恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
)的值域为R;命题q:3x﹣9x<a对一切实数x恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出两个命题:
命题甲:关于x的不等式x2+(a﹣1)x+a2≤0的解集为;
命题乙:函数y=(2a2﹣a)x为增函数.
(1)甲、乙至少有一个是真命题;
(2)甲、乙有且只有一个是真命题;
分别求出符合(1)(2)的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,D是到原点的距离不大于1的点构成的区域,E是满足不等式组  的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次试验中,两个试验数据x,y的统计结果如下面的表格1所示.
x | 1 | 2 | 3 | 4 | 5 |
y | 2 | 3 | 4 | 4 | 5 |
表格1

(1)在给出的坐标系中画出数据x,y的散点图.
(2)补全表格2,根据表格2中的数据和公式 求下列问题.
求下列问题.
①求出y关于x的回归直线方程![]() 中的
中的![]() .
.
②估计当x=10时,![]() 的值是多少?
的值是多少?
表格2
序号 | x | y | x2 | xy |
1 | 1 | 2 | 1 | 2 |
2 | 2 | 3 | 4 | 6 |
3 | 3 | 4 | 9 | 12 |
4 | 4 | 4 | 16 | 16 |
5 | 5 | 5 | 25 | 25 |
∑ |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2)
=1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2) 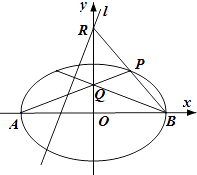
(1)求椭圆C的标准方程;
(2)求证: ![]() 为定值;
为定值;
(3)求证:过点R且与直线QB垂直的直线经过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q. 
(1)若直线l的斜率为 ![]() ,求
,求 ![]() 的值;
的值;
(2)若 ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com