
【题目】如图,几何体![]() 中,
中,![]() 为边长为2的正方形,
为边长为2的正方形,![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的大小.
的大小.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥![]() 中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且
中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且![]() .
.
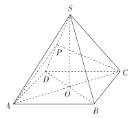
(1)证明:![]() 平面PAC.
平面PAC.
(2)求直线BC与平面PAC的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级开设了丰富多彩的校本课程,现从甲、乙两个班随机抽取了5名学生校本课程的学分,统计如下表.
甲 | 8 | 11 | 14 | 15 | 22 |
乙 | 6 | 7 | 10 | 23 | 24 |
用![]() 分别表示甲、乙两班抽取的5名学生学分的方差,计算两个班学分的方差.得
分别表示甲、乙两班抽取的5名学生学分的方差,计算两个班学分的方差.得![]() ______,并由此可判断成绩更稳定的班级是______班.
______,并由此可判断成绩更稳定的班级是______班.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,
,![]() 是长轴的一个端点,弦
是长轴的一个端点,弦![]() 过椭圆的中心
过椭圆的中心![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程.
的方程.
(2)过椭圆![]() 右焦点
右焦点![]() 的直线,交椭圆
的直线,交椭圆![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() ,判定直线
,判定直线![]() 的斜率是否依次构成等差数列?请说明理由.
的斜率是否依次构成等差数列?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从6名男医生和3名女医生中选出5人组成一个医疗小组,请解答下列问题:
(1)如果这个医疗小组中男女医生都不能少于2人,共有多少种不同的建组方案?(用数字作答)
(2)男医生甲要担任医疗小组组长,所以必选,而且医疗小组必须男女医生都有,共有多少种不同的建组方案?
(3)男医生甲与女医生乙不被同时选中的概率.(化成最简分数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当时
的图象.当时![]() ,求函数
,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
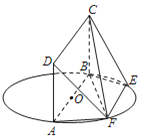
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)当AD=1时,求直线FB与平面DFC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜批发商分别在甲、乙两市场销售某种蔬菜(两个市场的销售互不影响),己知该蔬菜每售出1吨获利500元,未售出的蔬菜低价处理,每吨亏损100 元.现统计甲、乙两市场以往100个销售周期该蔬菜的市场需求量的频数分布,如下表:
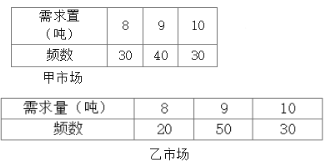
以市场需求量的频率代替需求量的概率.设批发商在下个销售周期购进![]() 吨该蔬菜,在 甲、乙两市场同时销售,以
吨该蔬菜,在 甲、乙两市场同时销售,以![]() (单位:吨)表示下个销售周期两市场的需求量,
(单位:吨)表示下个销售周期两市场的需求量,![]() (单位:元)表示下个销售周期两市场的销售总利润.
(单位:元)表示下个销售周期两市场的销售总利润.
(Ⅰ)当![]() 时,求
时,求![]() 与
与![]() 的函数解析式,并估计销售利润不少于8900元的槪率;
的函数解析式,并估计销售利润不少于8900元的槪率;
(Ⅱ)以销售利润的期望为决策依据,判断![]() 与
与![]() 应选用哪—个.
应选用哪—个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,圆
,圆![]() 上有一动点
上有一动点![]() ,
,![]() 在
在![]() 轴上方,点
轴上方,点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
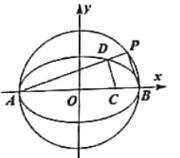
(1)若![]() ,求
,求![]() 的面积
的面积![]() ;
;
(2)设直线![]() ,
,![]() 的斜率存在且分别为
的斜率存在且分别为![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com