
【题目】已知数列{an}满足a1=9,an+1=an+2n+5;数列{bn}满足b1= ![]() ,bn+1=
,bn+1= ![]() bn(n≥1).
bn(n≥1).
(1)求an , bn;
(2)记数列{ ![]() }的前n项和为Sn , 证明:
}的前n项和为Sn , 证明: ![]() ≤Sn<
≤Sn< ![]() .
.
【答案】
(1)解:由an+1=an+2n+5得an+1﹣an=2n+5,
则a2﹣a1=7,
a3﹣a2=9,
…
an﹣1﹣an﹣2=2(n﹣2)+5,
an﹣an﹣1=2(n﹣1)+5=2n+3
等式两边同时相加得
an﹣a1= ![]() ×(n﹣1)=(5+n)(n﹣1)=n2+4n﹣5,
×(n﹣1)=(5+n)(n﹣1)=n2+4n﹣5,
则an=a1+n2+4n﹣5=n2+4n﹣5+9=n2+4n+4,
所以数列{an}的通项公式为 ![]() .
.
又∵ ![]() ,
, ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
,
将上述(n﹣1)个式子相乘,得 ![]() ,即
,即 ![]() .
.
(2)解:∵ ![]() .
.
∵ ![]() =
= ![]() ,
,
![]() ,∴
,∴ ![]()
【解析】(1)利用数列的递推关系,利用累加法和累积法进行求解即可.(2)求出数列{ ![]() }的通项公式,利用裂项法进行求解,结合不等式的性质进行证明即可.
}的通项公式,利用裂项法进行求解,结合不等式的性质进行证明即可.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系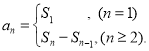 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
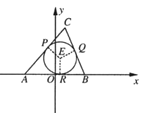
【题目】已知△ABC的两顶点坐标A(﹣1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M.
(I)求曲线M的方程;
(Ⅱ)设直线BC与曲线M的另一交点为D,当点A在以线段CD为直径的圆上时,求直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点.
上的点.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等比数列,a1=1,a6=243.Sn为等差数列{bn}的前n项和,b1=1,S5=25.
(1)求{an}和{bn}的通项公式;
(2)设Tn=a1b1+a2b2+…+anbn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式mx2+2x+6m>0,在下列条件下分别求m的值或取值范围:
(1)不等式的解集为{x|2<x<3};
(2)不等式的解集为R.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式an;
(2)若a3 , a5分别是等差数列{bn}的第4项和第16项,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com