
【题目】已知抛物线C:![]() 的焦点为F,抛物线C与直线l1:
的焦点为F,抛物线C与直线l1:![]() 的一个交点为
的一个交点为![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(Ⅰ)求抛物线C的方程;
(II)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A,B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
【答案】(I) y2=8x;(II)24![]()
【解析】
(I)确定抛物线C与直线l1:y=﹣x的一个交点的坐标,代入抛物线方程,即可求抛物线C方程;
(II)设l2的方程为x=y+m,代入抛物线方程,利用韦达定理,结合OA⊥OB,求出m的值,从而可求△FAB的面积.
解:(I)易知直线与抛物线的交点坐标为(8,-8),
∴(-8)2=2p×8,∴2p=8,∴抛物线方程为y2=8x.
(II)直线l2与l1垂直,故可设直线l2:x=y+m,A(x1,y1),B(x2,y2),且直线l2与x轴的交点为M.
由![]() 得y2-8y-8m=0,
得y2-8y-8m=0,
Δ=64+32m>0,∴m>-2.
y1+y2=8,y1y2=-8m,
∴x1x2=![]() =m2.
=m2.
由题意可知OA⊥OB,即x1x2+y1y2=m2-8m=0,
∴m=8或m=0(舍),
∴直线l2:x=y+8,M(8,0).
故S△FAB=S△FMB+S△FMA=![]() ·|FM|·|y1-y2|
·|FM|·|y1-y2|
=3![]() =24
=24![]() .
.


科目:高中数学 来源: 题型:
【题目】某班主任为了对本班学生的月考成绩进行分析,从全班40名同学中随机抽取一个容量为6的样本进行分析.随机抽取6位同学的数学、物理分数对应如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学分数x | 60 | 70 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 80 | 88 | 90 | 85 | 95 |
(1)根据上表数据用散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?
(2)如果具有线性相关性,求出线性回归方程(系数精确到0.1);如果不具有线性相关性,请说明理由.
(3)如果班里的某位同学数学成绩为50,请预测这位同学的物理成绩。
![]() (附
(附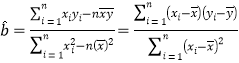 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其“无故障使用时间![]() (单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
(单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
无故障使用时间 |
|
|
|
频数 | 20 | 40 | 40 |
以试验结果中无故障使用时间落入各组的频率作为一件产品的无故障使用时间落入相应组的概率.
(1)从该企业任取两件这种产品,求至少有一件是优质品的概率;
(2)若该企业生产的这种产品每件销售利润![]() (单位:元)与其无故障使用时间
(单位:元)与其无故障使用时间![]() 的关系式为
的关系式为
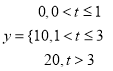
从该企业任取两件这种产品,其利润记为![]() (单位:元),求
(单位:元),求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,∠ABB1=60°.
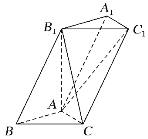
(I) 证明:AB⊥平面AB1C;
(II) 若B1C=2,求AC1与平面BCB1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
(t为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)求直线l和曲线C的直角坐标方程,并指明曲线C的形状;
(Ⅱ)设直线l与曲线C交于A,B两点,O为坐标原点,且|OA|<|OB|,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国第一高摩天轮“南昌之星摩天轮”高度为![]() ,其中心
,其中心![]() 距地面
距地面![]() ,半径为
,半径为![]() ,若某人从最低点
,若某人从最低点![]() 处登上摩天轮,摩天轮匀速旋转,那么此人与地面的距离将随时间
处登上摩天轮,摩天轮匀速旋转,那么此人与地面的距离将随时间![]() 变化,
变化,![]() 后达到最高点,从登上摩天轮时开始计时.
后达到最高点,从登上摩天轮时开始计时.
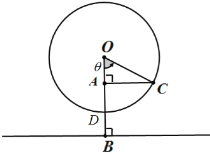
(1)求出人与地面距离![]() 与时间
与时间![]() 的函数解析式;
的函数解析式;
(2)从登上摩天轮到旋转一周过程中,有多长时间人与地面距离大于![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com