
已知椭圆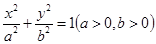 的左焦点F为圆
的左焦点F为圆 的圆心,且椭圆上的点到点F的距离最小值为
的圆心,且椭圆上的点到点F的距离最小值为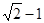 。
。
(I)求椭圆方程;
(II)已知经过点F的动直线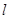 与椭圆交于不同的两点A、B,点M(
与椭圆交于不同的两点A、B,点M(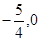 ),证明:
),证明: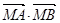 为定值。
为定值。
(I) (II)当直线
(II)当直线 与
与 轴垂直时,
轴垂直时, 的方程为
的方程为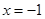
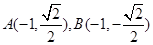
 ,当直线
,当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为 ,由
,由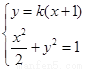 得
得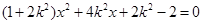 ,
,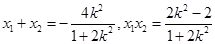 ,
, ,所以,
,所以,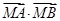 为定值,且定值为
为定值,且定值为
【解析】
试题分析:(1)因为圆 的圆心为
的圆心为 ,半径
,半径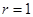 ,所以椭圆的半焦距
,所以椭圆的半焦距
又椭圆上的点到点F的距离最小值为 ,所以
,所以 ,即
,即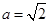
所以,所求椭圆的方程为 2分
2分
(2)①当直线 与
与 轴垂直时,
轴垂直时, 的方程为
的方程为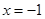 ,可求得
,可求得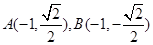
此时, 4分
4分
②当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为
由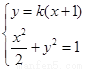 得
得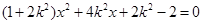 6分
6分
设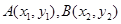 ,则
,则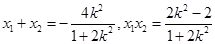 7分
7分
因为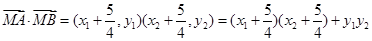
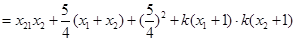

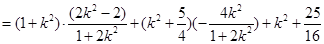


所以,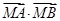 为定值,且定值为
为定值,且定值为 13分
13分
考点:椭圆方程性质及直线与椭圆的位置关系
点评:本题第二问中直线与椭圆相交时需注意讨论直线斜率存在与不存在两种情况,当斜率存在时常联立方程组,利用根与系数的关系求解化简


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
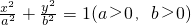 的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为
的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为 .
.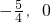 ),证明:
),证明: 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省潍坊市高三(上)期末数学试卷(文科)(解析版) 题型:解答题
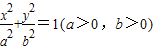 的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为
的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为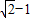 .
.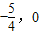 ),证明:
),证明: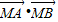 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省淄博市高三(上)期末数学试卷(文科)(解析版) 题型:解答题
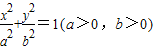 的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为
的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为 .
. ),证明:
),证明: 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源:2011年广东省深圳市高考数学一模试卷(文科)(解析版) 题型:解答题
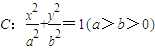 的左焦点F及点A(0,b),原点O到直线FA的距离为
的左焦点F及点A(0,b),原点O到直线FA的距离为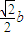 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com