
【题目】“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 平行”的( )
平行”的( )
A. 充要条件 B. 充分而不必要条件
C. 必要而不充分条件 D. 既不充分也不必要条件
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】如图所示四棱锥![]() 的底面为正方形,
的底面为正方形,![]() 平面
平面![]() 则下列结论中不正确的是( )
则下列结论中不正确的是( )

A.![]() B.
B.![]() 平面
平面![]()
C.直线![]() 与平面
与平面![]() 所成的角等于30°D.SA与平面SBD所成的角等于SC与平面SBD所成的角
所成的角等于30°D.SA与平面SBD所成的角等于SC与平面SBD所成的角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段![]() (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
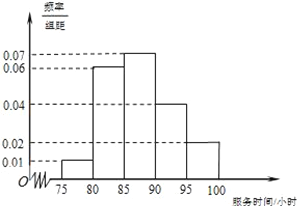
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上依次排列着![]() 共2013个不同的点,每个点染红、蓝、绿三色之一.在以任意两个同色点为端点的圆弧上,与此两端点异色的点的个数为偶数的染色方法称为“好染色”问:所有好染色方法有多少种?
共2013个不同的点,每个点染红、蓝、绿三色之一.在以任意两个同色点为端点的圆弧上,与此两端点异色的点的个数为偶数的染色方法称为“好染色”问:所有好染色方法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC中点,PO⊥平面ABCD,PO=2,M为PD中点.

(Ⅰ)证明:PB∥平面ACM;
(Ⅱ)证明:AD⊥平面PAC;
(Ⅲ)求直线AM与平面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥O﹣ABCD中,OA⊥底面ABCD,且底面ABCD是边长为2的正方形,且OA=2,M,N分别为OA,BC的中点.
(1)求证:直线MN![]() 平面OCD;
平面OCD;
(2)求点B到平面DMN的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 为其焦点,抛物线的准线交
为其焦点,抛物线的准线交![]() 轴于点T,直线l交抛物线于A,B两点。
轴于点T,直线l交抛物线于A,B两点。
(1)若O为坐标原点,直线l过抛物线焦点,且![]() ,求△AOB的面积;
,求△AOB的面积;
(2)当直线l与坐标轴不垂直时,若点B关于x轴的对称点在直线AT上,证明直线l过定点,并求出该定点的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的一个最高点为
的一个最高点为![]() ,与点
,与点![]() 相邻一个最低点为
相邻一个最低点为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)若![]() 时,函数
时,函数![]() 恰有一个零点,求实数
恰有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com