
【题目】甲乙两人各有相同的小球10个,在每人的10个小球中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
【答案】解:先考虑甲获胜的概率,甲获胜有一下几种情况:
(1)两个小球上的数字均为1,此时,甲获胜的概率为![]()
(2)两个小球上的数字均为2,此时,甲获胜的概率为![]()
(3)两个小球上的数字均为2,此时,甲获胜的概率为![]()
所以:甲获胜的概率![]()
![]()
故乙获胜的概率为![]()
![]()
【解析】
根据已知中若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,我们可由甲获胜和乙获胜互为对立事件,我们可以先求出甲获胜的概率,再根据对立事件概率减法公式,得到答案.
先考虑甲获胜的概率,甲获胜有一下几种情况:
(1)两个小球上的数字均为1,此时,甲获胜的概率为![]()
(2)两个小球上的数字均为2,此时,甲获胜的概率为![]()
(3)两个小球上的数字均为2,此时,甲获胜的概率为![]()
所以甲获胜的概率![]() =0.38,
=0.38,
故乙获胜的概率为![]() =0.62.
=0.62.


科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的中位数是83,乙班学生成绩的平均数是86,则x+y的值为( ) 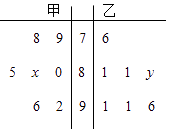
A.168
B.169
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x>0).
(x>0).
(1)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(2)若f(x)> ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n﹣3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)
①y= ![]() ;②y=
;②y=  ;③y=
;③y= ![]() ;④y=
;④y=  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数fn(x)=﹣xn+3ax(a∈R,n∈N+),若对任意的x1 , x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,则a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC. 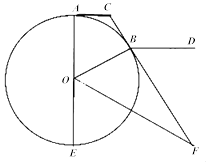
(1)证明:OB2=BCBF;
(2)证明:∠DBF=∠AOB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC. 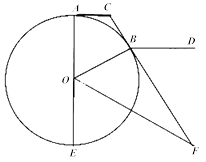
(1)证明:OB2=BCBF;
(2)证明:∠DBF=∠AOB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:y2=2x﹣4.
(1)求曲线C在点A(3, ![]() )处的切线方程;
)处的切线方程;
(2)过原点O作直线l与曲线C交于A,B两不同点,求线段AB的中点M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com