
【题目】给出下列命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,
,![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() ;④
;④![]() ;⑤若
;⑤若![]() ,
,![]() ,则
,则![]() ,
,![]() ;⑥正数
;⑥正数![]() ,
,![]() 满足
满足![]() ,则
,则![]() 的最小值为
的最小值为![]() .其中正确命题的序号是__________.
.其中正确命题的序号是__________.
【答案】②③④⑤
【解析】分析:利用不等式的性质与基本不等式对①②③④⑤⑥逐项判断即可.
详解:①若a<b<0,则![]() ,故①错误;
,故①错误;
②若a>0,b>0,则![]() ≥
≥![]() (当且仅当a=b时取等号);
(当且仅当a=b时取等号);
又![]() ﹣
﹣![]() =
=![]() (1﹣
(1﹣![]() )≥
)≥![]() (1﹣
(1﹣![]() )=
)=![]()
![]() >0≥0,
>0≥0,
所以![]() ≥
≥![]() ,综上,
,综上,![]() ≥
≥![]() ≥
≥![]() ,故②正确;
,故②正确;
③若a<b<0,则a2>ab>0,ab>b2>0,
因此,a2>ab>b2,故③正确;
④lg9lg 11<(![]() )2=
)2=![]() <
<![]() =1,故④正确;
=1,故④正确;
⑤若a>b,![]() >
>![]()
![]() ﹣
﹣![]() >0
>0![]() >0
>0![]() <0,则ab<0,所以a>0,b<0,故⑤正确;
<0,则ab<0,所以a>0,b<0,故⑤正确;
⑥正数x,y满足![]() +
+![]() =1,则x+2y=(x+2y)(
=1,则x+2y=(x+2y)(![]() +
+![]() )=1+2+
)=1+2+![]() +
+![]() ≥3+2
≥3+2![]() ,故其最小值为3+2
,故其最小值为3+2![]() ,故⑥错误.
,故⑥错误.
综上所述,正确命题的序号是:②③④⑤,
故答案为:②③④⑤.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]()
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上有且只有一个极值点,求实数
在定义域上有且只有一个极值点,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合,且两个坐标系的单位长度相同.已知直线l的参数方程为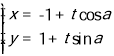 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(Ⅱ)若直线l与曲线C相交弦长为![]() ,求直线l的参数方程(标准形式).
,求直线l的参数方程(标准形式).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在函数
在函数![]() 的图象上,数列
的图象上,数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(![]() )求数列
)求数列![]() 的通项公式.
的通项公式.
(![]() )设
)设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .求数列
.求数列![]() 的前
的前![]() 项和
项和![]() .
.
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() 是定义在正整数集上的函数,对于任意的正整数
是定义在正整数集上的函数,对于任意的正整数![]() ,
,![]() ,恒有
,恒有![]() 成立,且
成立,且![]() (
(![]() 为常数,
为常数,![]() ),试判断数列
),试判断数列 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过底面是矩形的四棱锥FABCD的顶点F作EF∥AB,使AB=2EF,且平面ABFE⊥平面ABCD,若点G在CD上且满足DG=G![]() .
.
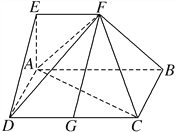
求证:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的左焦点为
的左焦点为![]() ,且过点
,且过点 .
.
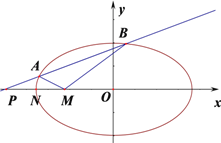
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线![]() 与椭圆E交于
与椭圆E交于![]() 两点,与
两点,与![]() 的交点为
的交点为![]() ,且满足.
,且满足. ![]()
![]()
①若![]() ,求:
,求: ![]() 的值;
的值;
②设点![]() 是椭圆E的左顶点,点
是椭圆E的左顶点,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,试探究:在线段
,试探究:在线段![]() 上是否存在一个定点
上是否存在一个定点![]() ,使得直线
,使得直线![]() 过定点
过定点![]() ,如果存在,求出点
,如果存在,求出点![]() 的坐标;如果不存在,请说明理由。
的坐标;如果不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有大小形状完全相同的5个小球,其中3个白球的标号分别为1、 2 、3, 2 个黑球的标号分别为1、3.
(Ⅰ)从袋中随机摸出两个球,求摸到的两球颜色与标号都不相同的概率;
(Ⅱ)从袋中有放回地摸球,摸两次,每次摸出一个球,求摸出的两球的标号之和小于4 的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com