
【题目】已知方向向量为v=(1, ![]() )的直线l过点(0,﹣2
)的直线l过点(0,﹣2 ![]() )和椭圆C:
)和椭圆C: ![]() =1(a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
=1(a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在过点E(﹣2,0)的直线m交椭圆C于点M、N,满足 ![]() =
= ![]() .cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
.cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
【答案】解:(I)解法一:直线l:y= ![]() x﹣2
x﹣2 ![]() ,①
,①
过原点垂直l的直线方程为y=﹣ ![]() x,②
x,②
解①②得x= ![]() .
.
∵椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,∴ ![]() =2×
=2× ![]() =3.
=3.
∵直线l过椭圆焦点,∴该焦点坐标为(2,0).∴c=2,a2=6,b2=2.故椭圆C的方程为 ![]() +
+ ![]() =1③
=1③
解法二:直线l:y= ![]() x﹣3
x﹣3 ![]() .
.
设原点关于直线l对称点为(p,q),则  解得p=3.
解得p=3.
∵椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,∴ ![]() =3.
=3.
∵直线l过椭圆焦点,∴该焦点坐标为(2,0).∴c=2,a2=6,b2=2.故椭圆C的方程为 ![]() +
+ ![]() =1③
=1③
(II)解:设M(x1 , y1),N(x2 , y2).
当直线m不垂直x轴时,直线m:y=k(x+2)代入③,
整理得(3k2+1)x2+12k2x+12k2﹣6=0,
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
|MN|= ![]() =
= 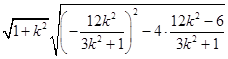 =
= ![]() ,
,
点O到直线MN的距离d= ![]() .
.
∵ ![]() =
= ![]() cot∠MON,即|
cot∠MON,即| ![]() ||
|| ![]() |cos∠MON=
|cos∠MON= ![]() ≠0,
≠0,
∴| ![]() ||
|| ![]() |sin∠MON=4
|sin∠MON=4 ![]() ,∴S△OMN=
,∴S△OMN= ![]() .∴|MN|d=
.∴|MN|d= ![]() ,
,
即4 ![]() |k|
|k| ![]() =
= ![]() (3k2+1),
(3k2+1),
整理得k2= ![]() ,∴k=±
,∴k=± ![]() .
.
当直线m垂直x轴时,也满足S△OMN= ![]() .
.
故直线m的方程为y= ![]() x+
x+ ![]() ,或y=﹣
,或y=﹣ ![]() x﹣
x﹣ ![]() ,或x=﹣2.
,或x=﹣2.
经检验上述直线均满足 ![]() ≠0.
≠0.
所以所求直线方程为y= ![]() x+
x+ ![]() ,或y=﹣
,或y=﹣ ![]() x﹣
x﹣ ![]() ,或x=﹣2.
,或x=﹣2.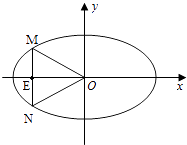

【解析】(I)解法一:直线l:y= ![]() x﹣2
x﹣2 ![]() ,过原点垂直l的直线方程为y=﹣
,过原点垂直l的直线方程为y=﹣ ![]() x,这两个方程联立可知x=
x,这两个方程联立可知x= ![]() .再由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,可知
.再由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,可知 ![]() =3.由此可以求出椭圆C的方程.
=3.由此可以求出椭圆C的方程.
解法二:直线l:y= ![]() x﹣3
x﹣3 ![]() .设原点关于直线l对称点为(p,q),则
.设原点关于直线l对称点为(p,q),则  解得p=3.由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,知
解得p=3.由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,知 ![]() =3.由此能够推出椭圆C的方程.(II)解:设M(x1 , y1),N(x2 , y2).当直线m不垂直x轴时,直线m:y=k(x+2)代入
=3.由此能够推出椭圆C的方程.(II)解:设M(x1 , y1),N(x2 , y2).当直线m不垂直x轴时,直线m:y=k(x+2)代入 ![]() +
+ ![]() =1,整理得(3k2+1)x2+12k2x+12k2﹣6=0,再由根与系数的关系和点到直线 的距离求解.
=1,整理得(3k2+1)x2+12k2x+12k2﹣6=0,再由根与系数的关系和点到直线 的距离求解.


科目:高中数学 来源: 题型:
【题目】某机构为了研究人的脚的大小与身高之间的关系,随机测量了20人,得到如下数据:


(1) 若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”,请根据上表数据完成下面的2×2列联表.

(2)根据(1)中的2×2列联表,在犯错误的概率不超过0.01的前提下,能否认为脚的大小与身高之间有关系?
![]() ,
,
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,l是过定点P(4,2)且倾斜角为α的直线;在极坐标系(以坐标原点O为极点,
以x轴非负半轴为极轴,取相同单位长度)中,曲线C的极坐标方程为![]() .
.
(1)写出直线l的参数方程,并将曲线C的方程化为直角坐标方程;
(2)若曲线C与直线相交于不同的两点M,N,求|PM|+|PN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个小组各10名学生的英语口语测试成绩如下(单位:分).
甲组:76,90,84,86,81,87,86,82,85,83 乙组:82,84,85,89,79,80,91,89,79,74
现从这20名学生中随机抽取一人,将“抽出的学生为甲组学生”记为事件A;“抽出学生的英语口语测试成绩不低于85分”记为事件B,则P(AB)、P(A|B)的值分别是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=1,AB=2,SD= ![]() .
. 
(1)求证:CD⊥平面ADS;
(2)求AD与SB所成角的余弦值;
(3)求二面角A﹣SB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出的命题中:
(1)“双曲线的方程为![]() ”是“双曲线的渐近线为
”是“双曲线的渐近线为![]() ”的充分不必要条件;
”的充分不必要条件;
(2)“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 互相垂直”的必要不充分条件;
互相垂直”的必要不充分条件;
(3)已知随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() ;
;
(4)已知圆![]() ,圆
,圆![]() ,则这两个圆有3条公切线.
,则这两个圆有3条公切线.
其中真命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,![]() 获得本场比赛胜利,最终人机大战总比分定格1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
获得本场比赛胜利,最终人机大战总比分定格1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(Ⅰ)根据已知条件完成列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?

非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名淡定生中的“围棋迷”人数为X。若每次抽取的结果是相互独立的,求X的分布列,期望 E(X) 和方差 D(X) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com