
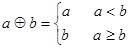 若函数
若函数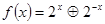 .
.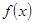 的解析式;
的解析式;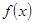 的图像,并指出单调区间、值域以及奇偶性.
的图像,并指出单调区间、值域以及奇偶性.科目:高中数学 来源:不详 题型:解答题
 元.公司拟投入
元.公司拟投入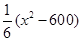 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过 年,树林中有木材
年,树林中有木材
 ,
, (
( )与
)与 之间的函数关系式。
之间的函数关系式。 ?(结果保留一个有效数字)
?(结果保留一个有效数字) ,
, )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 关于时间
关于时间 的函数关系式分别为
的函数关系式分别为 ,
, ,
, ,
, ,有以下结论:
,有以下结论: 时,甲走在最前面;
时,甲走在最前面; 时,乙走在最前面;
时,乙走在最前面; 时,丁走在最前面,当
时,丁走在最前面,当 时,丁走在最后面;
时,丁走在最后面;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com