
【题目】为了了解我国各景点在大众中的熟知度,随机对![]() ~
~![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组[ | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
![]()
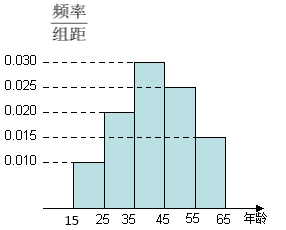
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组各抽取多少人;
组每组各抽取多少人;
(3)在(2)的条件下抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求所抽取的人中恰好没有第
人,求所抽取的人中恰好没有第![]() 组人的概率.
组人的概率.
【答案】(1)![]() ;(2)第
;(2)第![]() 中分别抽出
中分别抽出![]() 人,
人,![]() 人,
人,![]() 人;(3)
人;(3)![]() .
.
【解析】
试题分析:(1)观察表格,从第,![]() 组频数为
组频数为![]() ,频率为
,频率为![]() 可知,所以第四组
可知,所以第四组![]() 人,而由频率分布直方图可知,第四组的频率为
人,而由频率分布直方图可知,第四组的频率为![]() ,所以总人数
,所以总人数![]() 人,根据频率分布直方图可知,第
人,根据频率分布直方图可知,第![]() 组频率分别为
组频率分别为![]() ,所以这四组的人数分别为
,所以这四组的人数分别为![]() 人,则可以分别计算得到
人,则可以分别计算得到![]() ,
,![]() ,
,![]() ,
,![]() ;(2)根据第(1)问可知,第
;(2)根据第(1)问可知,第![]() 组回答正确人数之比为
组回答正确人数之比为![]() ,所以若按分层抽样方法从这三组中抽取
,所以若按分层抽样方法从这三组中抽取![]() 人,应从
人,应从![]() 中分别抽出
中分别抽出![]() 人,
人,![]() 人,
人,![]() 人;(3)设第
人;(3)设第![]() 组两人为
组两人为![]() ,第
,第![]() 组三人为
组三人为![]() ,第
,第![]() 组一人为
组一人为![]() ,则从
,则从![]() 人中任意抽取
人中任意抽取![]() 人工包含
人工包含![]() 个基本事件,其中恰好没有第
个基本事件,其中恰好没有第![]() 组人共包含
组人共包含![]() 个基本事件,所以根据古典概型概率公式有
个基本事件,所以根据古典概型概率公式有![]() .
.
试题解析:(1)由频率表中第4组数据可知,第4组总人数为![]() ,
,
再结合频率分布直方图可知![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
(2)因为第2,3,4组回答正确的人数共有54人,
所以利用分层抽样在54人中抽取6人,每组分别抽取的人数为:
第2组:![]() 人;第3组:
人;第3组:![]() 人;第4组:
人;第4组:![]() 人
人
(3)设第2组2人为:A1,A2;第3组3人为:B1,B2,B3;第4组1人为:C1.
则从6人中随机抽取2人的所有可能的结果为:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2, B2),(A2,B3),(A2,C1),(B1,B2),(B1,B3),(B1,C1),(B2,B3),(B2,C1),(B3,C1)
共15个基本事件
其中恰好没有第3组人共3个基本事件(A1,A2),(A2,C1),(A1,C1),
∴所抽取的人中恰好没有第3组人的概率是:![]() .
.


科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
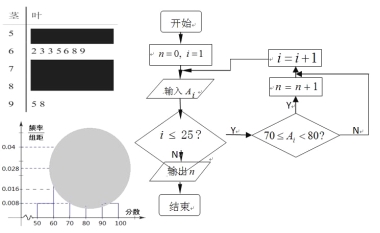
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各种情况下,向量终点构成什么图形?
(1)把所有单位向量的起点平移到同一点![]() ;
;
(2)把平行于某一直线的所有单位向量的起点平移到同一点;
(3)把平行于某一直线的一切向量平移到同一起点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.
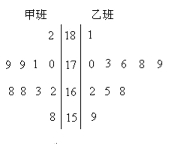
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:22,23,25,26,31,30;若B样本数据恰好是A样本中每个数据都减去10后所得的数据,则A,B两样本的下列数字特征相同的是( )
A.方差B.平均数C.众数D.中位数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有200名职工,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表:
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“使用微信交流”的态度与人的年龄有关:
的把握认为“使用微信交流”的态度与人的年龄有关:
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为
的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据如下:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考公式:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com