
【题目】函数![]() 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]() 内是单调函数;②
内是单调函数;②![]() 在
在![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 为
为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有_______
的“倍值区间”.下列函数中存在“倍值区间”的有_______
①![]() ②
②![]() ③
③![]()
【答案】①③
【解析】
根据”倍值区间”的定义,分别对三个函数研究,从而可确定存在”倍值区间”的函数.
对于①,假设函数![]() 存在”倍值区间”
存在”倍值区间”![]() ,因为函数
,因为函数![]() 为单调递增函数,
为单调递增函数,
所以![]() ,所以
,所以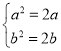 ,解得
,解得![]() ,
,
所以![]() 存在”倍值区间”
存在”倍值区间”![]() ;
;
对于②,假设函数![]() 存在”倍值区间”
存在”倍值区间”![]() ,因为
,因为![]() 为递增函数,
为递增函数,
所以![]() ,所以
,所以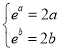 ,
,
构造函数![]() ,则
,则![]() ,
,
所以由![]() 得
得![]() ,
,![]() 递增;
递增;
由![]() 得
得![]() ,
,![]() 递减,
递减,
所以![]() 在
在![]() 时取得最小值,最小值为
时取得最小值,最小值为![]()
![]() ,
,
所以![]() 恒成立,所以
恒成立,所以![]() 无解,
无解,
故![]() 不存在”倍值区间”;
不存在”倍值区间”;
对于③,,假设函数存在”倍值区间”![]() ,因为
,因为![]() ,
,
所以![]()
![]() .
.
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
假设![]()
![]() ,
,
则函数![]() 在
在![]() 上递增,
上递增,
所以![]() ,所以
,所以 ,所以
,所以![]() ,
,
所以函数![]() 存在”倍值区间”
存在”倍值区间”![]() .
.
综上所述: 函数中存在“倍值区间”的有:①③.
故答案为:①③.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,且离心率为
(a>b>0)的左、右焦点分别为F1,F2,且离心率为![]() ,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A是椭圆C上异于椭圆顶点的一点,延长直线AF1,AF2分别与椭圆交于点B,D,设直线BD的斜率为k1,直线OA的斜率为k2,求证:k1·k2等于定值.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)由题意可求得![]() ,则
,则![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,
当直线![]() 的斜率不存在或直线
的斜率不存在或直线![]() 的斜率不存在时,
的斜率不存在时,![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立直线方程与椭圆方程,结合韦达定理计算可得直线
,联立直线方程与椭圆方程,结合韦达定理计算可得直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() .综上可得:直线
.综上可得:直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
(Ⅰ)设![]() 由题
由题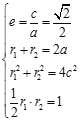 ,
,
解得![]() ,则
,则![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,当直线
,当直线![]() 的斜率不存在时,
的斜率不存在时,
设![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() 代入
代入![]() ,
,
可得![]()
![]() ,
,![]() ,则
,则![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
![]() ,
,
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() 设直线
设直线![]() 的方程为
的方程为![]() ,
,
则由 消去
消去![]() 可得:
可得:![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得:
,代入上述方程可得:
![]() ,
,![]() ,
,
则![]()
![]() ,
,
设直线![]() 的方程为
的方程为![]() ,同理可得
,同理可得![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,![]()
 .
.
所以,直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.
【点睛】
(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x(或y)建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.
(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.
【题型】解答题
【结束】
21
【题目】已知函数f(x)=(x+b)(![]() -a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
-a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
(Ⅰ)求a,b;
(Ⅱ)若方程f(x)=m有两个实数根x1,x2,且x1<x2,证明:x2-x1≤1+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,若集合A={y|y=3﹣2﹣x},B={x| ![]() ≤0},则A∩UB=( )
≤0},则A∩UB=( )
A.(﹣∞,0)∪[2,3)
B.(﹣∞,0]∪(2,3)
C.[0,2)
D.[0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的焦点分别为
=1(a>b>0)的焦点分别为 ![]() 、
、 ![]() ,点P在椭圆C上,满足|PF1|=7|PF2|,tan∠F1PF2=4
,点P在椭圆C上,满足|PF1|=7|PF2|,tan∠F1PF2=4 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A(1,0),试探究是否存在直线l:y=kx+m与椭圆C交于D、E两点,且使得|AD|=|AE|?若存在,求出k的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.

(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作出如图所示的等高条形图.

(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的中点值作为代表);
(2)根据已知条件完成下面的2×2列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
附:参考公式![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王老师的班上有四个体育健将甲、乙、丙、丁,他们都特别擅长短跑,在某次运动会上,他们四人要组成一个![]() 米接力队,王老师要安排他们四个人的出场顺序,以下是他们四人的对话:
米接力队,王老师要安排他们四个人的出场顺序,以下是他们四人的对话:
甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;
丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒;
王老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求, 据此我们可以断定,在王老师安排的出场顺序中,跑第三棒的人是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为 ![]() ,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.
,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.
(Ⅰ)求椭圆E的方程;
(Ⅱ)判断ABCD能否为菱形,并说明理由.
(Ⅲ)当ABCD的面积取到最大值时,判断ABCD的形状,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1底面是边长为1的正方形,高AA1= ![]() ,点A是平面α内的一个定点,AA1与α所成角为
,点A是平面α内的一个定点,AA1与α所成角为 ![]() ,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= .
,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com