
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)计算上线考生中抽取的男生成绩的方差![]() ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)
(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|1≤2x+5≤15}.
(1)已知a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
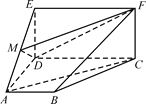
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现从中随机抽取100人的数学与地理的水平测试成绩如下表:
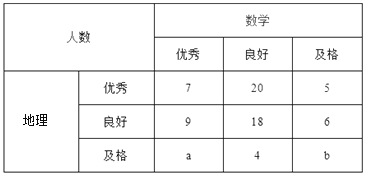
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有![]() .
.
(Ⅰ)若在该样本中,数学成绩优秀率是30%,求![]() 的值;
的值;
(Ⅱ)已知![]() ,求数学成绩为优秀的人数比及格的人数少的概率.
,求数学成绩为优秀的人数比及格的人数少的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com