
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() ),其图象相邻两条对称轴之间的距离为
),其图象相邻两条对称轴之间的距离为 ![]() ,且函数f(x+
,且函数f(x+ ![]() )是偶函数,下列判断正确的是( )
)是偶函数,下列判断正确的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)的图象关于点( ![]() ,0)d对称
,0)d对称
C.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
D.函数f(x)在[ ![]() ,π]上单调递增
,π]上单调递增
【答案】D
【解析】解:函数f(x)=sin(ωx+φ)图象的相邻两条对称轴之间的距离等于 ![]() ,
,
∴函数f(x)的周期T=π,故A错误;
∵ω>0
∴ω=2,
∴函数f(x+ ![]() )的解析式为:f(x)=sin[2(x+
)的解析式为:f(x)=sin[2(x+ ![]() )+φ]=sin(2x+
)+φ]=sin(2x+ ![]() +φ),
+φ),
∵函数f(x+ ![]() )是偶函数,
)是偶函数,
∴ ![]() +φ=kπ+
+φ=kπ+ ![]() ,k∈Z,又|φ|<
,k∈Z,又|φ|< ![]() ,解得:φ=
,解得:φ= ![]() .
.
∴f(x)=sin(2x+ ![]() ).
).
∴由2x+ ![]() =kπ,k∈Z,解得对称中心为:(
=kπ,k∈Z,解得对称中心为:( ![]() ﹣
﹣ ![]() ,0),k∈Z,故B错误;
,0),k∈Z,故B错误;
由2x+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,解得对称轴是:x=
,k∈Z,解得对称轴是:x= ![]() ,k∈Z,故C错误;
,k∈Z,故C错误;
由2kπ- ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,解得单调递增区间为:[kπ-
,k∈Z,解得单调递增区间为:[kπ- ![]() ,kπ+
,kπ+ ![]() ],k∈Z,故D正确.
],k∈Z,故D正确.
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,且a,b,﹣2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2. 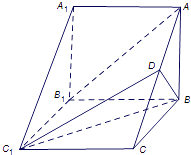
(1)求证:AB1∥平面BC1D;
(2)若BC=3,求三棱锥D﹣BC1C的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 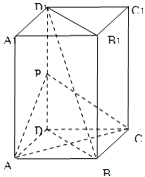
(1)求证:直线BD1∥平面PAC;
(2)求证:平面PAC⊥平面BDD1B1;
(3)求CP与平面BDD1B1所成的角大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= ![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,分别求a和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米, ![]() 米,记∠BHE=θ.
米,记∠BHE=θ. 
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若 ![]() ,求此时管道的长度L;
,求此时管道的长度L;
(3)当θ取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个点A(2,1)、B(3,2)、D(﹣1,4).
(1)求证: ![]() ;
;
(2)要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD两对角线所夹锐角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com