
【题目】在一次电视节目的答题游戏中,题型为选择题,只有“A”和“B”两种结果,其中某选手选择正确的概率为p,选择错误的概率为q,若选择正确则加1分,选择错误则减1分,现记“该选手答完n道题后总得分为![]() ”.
”.
(1)当![]() 时,记
时,记![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)当![]() ,
,![]() 时,求
时,求![]() 且
且![]() 的概率.
的概率.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
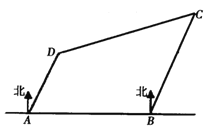
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 在区间
在区间![]() 单调递减;
单调递减;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 的最大值为
的最大值为![]() .
.
其中所有正确结论的编号是( )
A.①②④B.②④C.①④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .关于函数
.关于函数![]() 的零点,有下列三个命题:
的零点,有下列三个命题:
①当![]() 时,存在实数m,使函数
时,存在实数m,使函数![]() 恰有5个不同的零点;
恰有5个不同的零点;
②若![]() ,函数
,函数![]() 的零点不超过4个,则
的零点不超过4个,则![]() ;
;
③对![]() ,
,![]() ,函数
,函数![]() 恰有4个不同的零点,且这4个零点可以组成等差数列.
恰有4个不同的零点,且这4个零点可以组成等差数列.
其中,正确命题的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知平行于
中,已知平行于![]() 轴的动直线
轴的动直线![]() 交抛物线
交抛物线![]() :
: ![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的焦点.圆心不在
的焦点.圆心不在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() ,
, ![]() ,
, ![]() 轴都相切,设
轴都相切,设![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,过
,过![]() 且垂直于
且垂直于![]() 的直线为
的直线为![]() ,直线
,直线![]() ,
, ![]() 分别与
分别与![]() 轴相交于点
轴相交于点![]() ,
, ![]() .当线段
.当线段![]() 的长度最小时,求
的长度最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点曲线
的焦点曲线![]() 的一个焦点,
的一个焦点, ![]() 为坐标原点,点
为坐标原点,点![]() 为抛物线
为抛物线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的平行线交抛物线的准线于
轴的平行线交抛物线的准线于![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 过定点
过定点![]() ,并求出此定点的坐标.
,并求出此定点的坐标.
【答案】(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】试题分析:(Ⅰ)将曲线![]() 化为标准方程,可求得
化为标准方程,可求得![]() 的焦点坐标分别为
的焦点坐标分别为![]() ,可得
,可得![]() ,所以
,所以![]() ,即抛物线的方程为
,即抛物线的方程为![]() ;(Ⅱ)结合(Ⅰ),可设
;(Ⅱ)结合(Ⅰ),可设![]() ,得
,得 ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,解得
,解得![]() ,直线
,直线![]() 的方程为
的方程为 ,整理得
,整理得![]() 的方程为
的方程为![]() ,此时直线恒过定点
,此时直线恒过定点![]() .
.
试题解析:(Ⅰ)由曲线![]() ,化为标准方程可得
,化为标准方程可得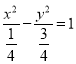 , 所以曲线
, 所以曲线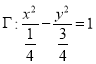 是焦点在
是焦点在![]() 轴上的双曲线,其中
轴上的双曲线,其中![]() ,故
,故![]() ,
, ![]() 的焦点坐标分别为
的焦点坐标分别为![]() ,因为抛物线的焦点坐标为
,因为抛物线的焦点坐标为![]() ,由题意知
,由题意知![]() ,所以
,所以![]() ,即抛物线的方程为
,即抛物线的方程为![]() .
.
(Ⅱ)由(Ⅰ)知抛物线![]() 的准线方程为
的准线方程为![]() ,设
,设![]() ,显然
,显然![]() .故
.故 ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,解得
,解得![]()
①当![]() ,即
,即![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,
②当![]() ,即
,即![]() 时,直线
时,直线![]() 的方程为
的方程为 ,整理得
,整理得![]() 的方程为
的方程为![]() ,此时直线恒过定点
,此时直线恒过定点![]() ,
, ![]() 也在直线
也在直线![]() 的方程为
的方程为![]() 上,故直线
上,故直线![]() 的方程恒过定点
的方程恒过定点![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若数列![]() 满足
满足![]() ,
, ![]() ,记
,记![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com