练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设△ABC的内角A、B、C的对边长分别为a、b、c，cos（A﹣C）+cosB= ，b2=ac，求B．

    【答案】解：由cos（A﹣C）+cosB= 及B=π﹣（A+C）得 cos（A﹣C）﹣cos（A+C）= ，
    ∴cosAcosC+sinAsinC﹣（cosAcosC﹣sinAsinC）= ，
    ∴sinAsinC= ．
    又由b2=ac及正弦定理得sin2B=sinAsinC，
    故 ，
    ∴ 或 （舍去），
    于是B= 或B= ．
    又由b2=ac
    知b≤a或b≤c
    所以B=
    【解析】本题考查三角函数化简及解三角形的能力，关键是注意角的范围对角的三角函数值的制约，并利用正弦定理得到sinB= （负值舍掉），从而求出答案．
    【考点精析】认真审题，首先需要了解同角三角函数基本关系的运用(同角三角函数的基本关系：；;（3） 倒数关系：)，还要掌握正弦定理的定义(正弦定理:)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分） 已知中心在原点，焦点在轴上的椭圆C的离心率为，且经过点．

    （1）求椭圆C的方程；

    （2）是否存在过点的直线与椭圆C相交于不同的两点，满足?若存在，求出直线的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

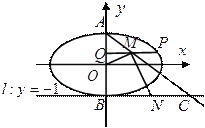
    【题目】如图，已知中心在原点，焦点在轴上的椭圆的一个焦点为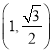， 是椭圆上的一个点．

    （1）求椭圆的标准方程；

    （2）设椭圆的上、下顶点分别为， （）是椭圆上异于的任意一点， 轴， 为垂足， 为线段中点，直线交直线于点, 为线段的中点，如果的面积为，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，记长方体ABCD﹣A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的几何体为Ω，则下列结论中不正确的是（ ）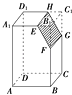

    A.EH∥FG
    B.四边形EFGH是平行四边形
    C.Ω是棱柱
    D.Ω是棱台

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， （）

    （Ⅰ）讨论的单调性；

    （Ⅱ）证明：当时，函数（）有最小值.记的最小值为，求的值域；

    （Ⅲ）若存在两个不同的零点， （），求的取值范围，并比较与0的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P﹣ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形．AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．
    （Ⅰ）求证：BE∥平面APD；
    （Ⅱ）求证：BC⊥平面PBD．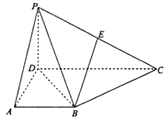

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD﹣A1B1C1D1中，M和N分别为BC、C1C的中点，那么异面直线MN与AC所成的角等于（ ）
    A.30°
    B.45°
    C.60°
    D.90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个简单几何体的主视图，左视图如图所示，则其俯视图不可能为( ) ．

    A.长方形
    B.直角三角形
    C.圆
    D.椭圆

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设向量 =（sinx，cosx）， =（cosx，sinx），x∈R，函数f（x）= （ ﹣ ）．
    （1）求函数f（x）的最小正周期；
    （2）当x∈[- ， ]时，求函数f（x）的值域．

    查看答案和解析>>

    同步练习册答案