
【题目】已知幂函数f(x)=x﹣m2+m+2(m∈Z)在(0,+∞)上单调递增.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)﹣ax+1,a为实常数,求g(x)在区间[﹣1,1]上的最小值.
【答案】解:(1)因为幂函数f(x)=x﹣m2+m+2 在(0,+∞)上单调递增,
所以﹣m2+m+2>0,故﹣1<m<2.
又因为m∈Z,故m=0,或m=1,所以f(x)=x2 .
(2)由(1)知g(x)=x2﹣ax+1,
①若![]() ≤﹣1,即a≤﹣2时,g(x)在[﹣1,1]上单调递增,
≤﹣1,即a≤﹣2时,g(x)在[﹣1,1]上单调递增,
所以g(x)mi n=g(﹣1)=a+2.
②若﹣1<![]() ≤1,即﹣2<a≤2时,
≤1,即﹣2<a≤2时,
g(x)在[﹣1,![]() ]上单调递减,[
]上单调递减,[![]() ,1]上单调递增,
,1]上单调递增,
所以g(x)min=g(\frac{a}{2})=1﹣![]() .
.
③若![]() >1,即a>2时,g(x)在[﹣1,1]上单调递减,
>1,即a>2时,g(x)在[﹣1,1]上单调递减,
所以g(x)min=g(1)=2﹣a.
综上:a≤﹣2时,g(x)在区间[﹣1,1]上的最小值为a+2;
﹣2<a≤2时,g(x)在区间[﹣1,1]上的最小值为1﹣![]() ;
;
a>2时,g(x)在区间[﹣1,1]上的最小值为2﹣a.
【解析】(1)由条件可得﹣m2+m+2>0,解得m的范围m.再结合m∈Z,求得m的值,可得f(x)的解析式.
(2)由(1)知g(x)=x2﹣ax+1,再分①若![]() ≤﹣1、②若﹣1<
≤﹣1、②若﹣1<![]() ≤1、③若
≤1、③若![]() >1三种情况,分别利用二次函数的性质,求得g(x)min . .
>1三种情况,分别利用二次函数的性质,求得g(x)min . .
【考点精析】解答此题的关键在于理解二次函数在闭区间上的最值的相关知识,掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的是( )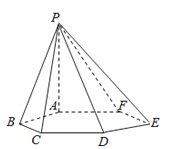
A.CD∥平面PAF
B.DF⊥平面PAF
C.CF∥平面PAB
D.CF⊥平面PAD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)=x2﹣2(a+2)x+a2 , g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max(p,q)表示p,q中的较大值,min(p,q)表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=( )
A.a2﹣2a﹣16
B.a2+2a﹣16
C.-16
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (x﹣2)的定义域为集合A,函数
(x﹣2)的定义域为集合A,函数![]() 的值域为集合B.
的值域为集合B.
(1)求A∪B;
(2)若集合C={x|a≤x≤3a﹣1},且B∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+2,x∈[﹣5,5]
(1)求实数a的取值范围,使y=f(x)在定义域上是单调递减函数;
(2)用g(a)表示函数y=f(x)的最小值,求g(a)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过![]()
![]() 关者奖励
关者奖励![]() 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
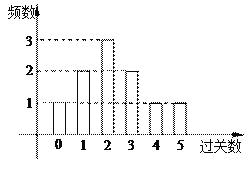
(Ⅰ)估计小明在1次游戏中所得奖品数的期望值;
(Ⅱ)估计小明在3 次游戏中至少过两关的平均次数;
(Ⅲ)估计小明在3 次游戏中所得奖品超过30件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程是
的方程是![]() ,双曲线
,双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() 的左右顶点,而
的左右顶点,而![]() 的左右顶点分别是
的左右顶点分别是![]() 的左右焦点.
的左右焦点.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点,且
恒有两个不同的交点,且![]() 与
与![]() 的两个交点A和B满足
的两个交点A和B满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com