
【题目】已知抛物线C:x2=2py(p>0),直线l1:y=kx+t与抛物线C交于A,B两点(A点在B点右侧),直线l2:y=kx+m(m≠t)交抛物线C于M,N两点(M点在N点右侧),直线AM与直线BN交于点E,交点E的横坐标为2k,则抛物线C的方程为( )
A.x2=yB.x2=2yC.x2=3yD.x2=4y
科目:高中数学 来源: 题型:
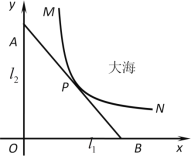
【题目】某沿海城市的海边有两条相互垂直的直线型公路![]() 、
、![]() ,海岸边界
,海岸边界![]() 近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道
近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段
有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段![]() 是函数
是函数![]() 图像的一段,点M到
图像的一段,点M到![]() 、
、![]() 的距离分别为8千米和1千米,点N到
的距离分别为8千米和1千米,点N到![]() 的距离为10千米,点P到
的距离为10千米,点P到![]() 的距离为2千米.以
的距离为2千米.以![]() 、
、![]() 分别为x,y轴建立如图所示的平面直角坐标系
分别为x,y轴建立如图所示的平面直角坐标系![]() .
.
(1)求曲线段![]() 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
(2)求直线![]() 的方程,并求出公路
的方程,并求出公路![]() 的长度(结果精确到1米).
的长度(结果精确到1米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
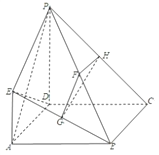
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列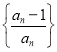 的前
的前![]() 项积,且
项积,且![]() ,求数列
,求数列![]() 的最大项.
的最大项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (a>b>0)的离心率e
(a>b>0)的离心率e![]() .
.
(1)若点P(1,![]() )在椭圆E上,求椭圆E的标准方程;
)在椭圆E上,求椭圆E的标准方程;
(2)若D(2,0)在椭圆内部,过点D斜率为![]() 的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以数列![]() 的任意相邻两项为坐标的点
的任意相邻两项为坐标的点![]() ,均在一次函数y=2x+k的图象上,数列
,均在一次函数y=2x+k的图象上,数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)求证数列![]() 为等比数列,并求出数列
为等比数列,并求出数列![]() 的公比;
的公比;
(2)设数列![]() ,
,![]() 的前n项和分别为Sn,Tn,若S6=T4,S5=﹣9,求k的值.
的前n项和分别为Sn,Tn,若S6=T4,S5=﹣9,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读参考材料,再解决此问题:
参考材料:求抛物线弧![]() (
(![]() )与x轴及直线
)与x轴及直线![]() 所围成的封闭图形的面积
所围成的封闭图形的面积
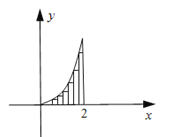
解:把区间![]() 进行n等分,得
进行n等分,得![]() 个分点
个分点![]() (
(![]() ),过分点
),过分点![]() ,作x轴的垂线,交抛物线于
,作x轴的垂线,交抛物线于![]() ,并如图构造
,并如图构造![]() 个矩形,先求出
个矩形,先求出![]() 个矩形的面积和
个矩形的面积和![]() ,再求
,再求![]() ,即是封闭图形的面积,又每个矩形的宽为
,即是封闭图形的面积,又每个矩形的宽为![]() ,第i个矩形的高为
,第i个矩形的高为![]() ,所以第i个矩形的面积为
,所以第i个矩形的面积为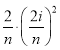 ;
;
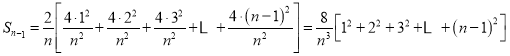
![]()
所以封闭图形的面积为![]()
阅读以上材料,并解决此问题:已知对任意大于4的正整数n,
不等式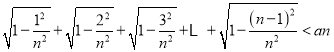 恒成立,
恒成立,
则实数a的取值范围为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()
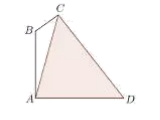
(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com