
【题目】某种零件按质量标准分为1,2,3,4,5五个等级,现从批该零件中随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
(1)在抽取的20个零件中,等级为5的恰有2个,求m,n的值;
(2)在(1)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级不相同的概率.
【答案】
(1)解:由频率分布表得:
0.05+m+.015+.035+n=1,
∴m+n=0.45
由抽取的20个零件中,等级为5的恰有2个,则n= ![]() =0.1,
=0.1,
∴m=0.450.1=0.35
(2)解:由(1)得等级为3的零件有3个,记作a,b,c,等级为5的零件有2个,记作A,B,
从等级为3和5的所有零件中,任意抽取2个,有
(a,b),(a,c),(a,A),(a,B),(b,c),
(b,A),(b,B),(a,A),(c,B),(A,B),共10种
记事件A为“抽取的2个零件等级不相同”,则A包含的基本事件是
(a,A),(a,B),(b,A),(b,B),(c,A),(c,B),共6个 ,
所求概率P(A)= ![]() =
= ![]() ,
,
即抽取的2个零件等级不相同的概率为 ![]()
【解析】(1)根据各组数据的累积频率为1,及频率= ![]() ,可构造关于m,n的方程,解方程可得m,n的值;(2)先计算从等级为3和5的零件中任取2人的基本事件总数及抽取的2个零件等级不相同的基本事件个数,代入古典概型概率计算公式,可得答案.
,可构造关于m,n的方程,解方程可得m,n的值;(2)先计算从等级为3和5的零件中任取2人的基本事件总数及抽取的2个零件等级不相同的基本事件个数,代入古典概型概率计算公式,可得答案.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() +
+ ![]() )x3(a>0,a≠1).
)x3(a>0,a≠1).
(1)讨论函数f(x)的奇偶性;
(2)求a的取值范围,使f(x)+f(2x)>0在其定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间D上的函数f(x),如果满足:对任意x∈D,都存在常数M≥0,有|f(x)|≤M,则称f(x)是区间D上有界函数,其中M称为f(x)上的一个上界,已知函数g(x)=log ![]() 为奇函数.
为奇函数.
(1)求函数g(x)在区间[ ![]() ,
, ![]() ]上的所有上界构成的集合;
]上的所有上界构成的集合;
(2)若g(1﹣m)+g(1﹣m2)<0,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AA1=BC=2AC=2. (Ⅰ)若D为AA1中点,求证:平面B1CD⊥平面B1C1D;
(Ⅱ)在AA1上是否存在一点D,使得二面角B1﹣CD﹣C1的大小为60°.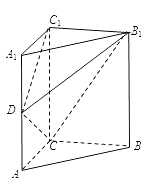
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足 ![]() ≤0。
≤0。
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥S﹣ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点. 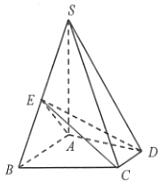
(1)求证:CE∥平面SAD;
(2)求二面角D﹣EC﹣B的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A﹣BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4 ![]() ,CD=4
,CD=4 ![]() ,∠ACB=45°,E,F分别为MN的中点.
,∠ACB=45°,E,F分别为MN的中点. 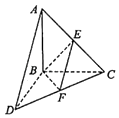
(1)求证:EF∥平面ABD;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() . (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
. (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com