
【题目】定义在R上的函数![]() 和二次函数
和二次函数![]() 满足:
满足:![]() ,
,![]() ,
,![]()
(1)求![]() 和
和![]() 的解析式;
的解析式;
(2)若对于![]() ,
,![]() ,均有
,均有![]() 成立,求a的取值范围;
成立,求a的取值范围;
(3)设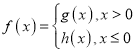 ,在(2)的条件下,讨论方程
,在(2)的条件下,讨论方程![]() 的解的个数.
的解的个数.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)通过![]() 代替
代替![]() ,推出方程,求解函数
,推出方程,求解函数![]() 的解析式.利用
的解析式.利用![]() 是二次函数,且
是二次函数,且![]() ,可设
,可设![]() ,然后求解即可.
,然后求解即可.
(2)设![]() ,
,![]() ,转化条件为当
,转化条件为当![]() 时,
时,![]() ,通过函数的单调性求解函数的最值,列出关系式即可求出实数
,通过函数的单调性求解函数的最值,列出关系式即可求出实数![]() 的取值范围.
的取值范围.
(3)设![]() ,由(2)知,画出函数在
,由(2)知,画出函数在![]() 的图象,设
的图象,设![]() ,则
,则![]() 当
当![]() ,当
,当![]() ,当
,当![]() ,当
,当![]() ,分别判断函数的图象交点个数,得到结论.
,分别判断函数的图象交点个数,得到结论.
解:(1)![]()
![]() ,①
,①![]() ,即
,即![]() ,②
,②
由①②联立解得:![]() .
.
![]() 是二次函数,且
是二次函数,且![]() ,可设
,可设![]() ,
,
由![]() ,解得
,解得![]() .
.
![]()
![]() ,
,![]() .
.
(2)设![]() ,
,![]() ,
,
依题意知:当![]() 时,
时,![]()
![]() ,在
,在![]() 上单调递增,
上单调递增,
![]()
![]()
![]() ,解得:
,解得:![]()
![]() 实数
实数![]() 的取值范围为
的取值范围为![]() .
.
(3)设![]() ,由(2)知,
,由(2)知,![]() 的图象如图所示:
的图象如图所示:
设![]() ,则
,则![]()
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,![]() 有两个 解,
有两个 解,![]() 有3个解;
有3个解;
当![]() ,即
,即![]() 时,
时,![]() 且
且![]() ,
,![]() 有3个解;
有3个解;
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 有2个解;
有2个解;
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 有1个解.
有1个解.
综上所述:
当![]() 时,方程有5个解;
时,方程有5个解;
当![]() 时,方程有3个解.
时,方程有3个解.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x.

(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补全函数f(x)的图象;
(2)求出函数f(x)(x>0)的解析式;
(3)若方程f(x)=a恰有3个不同的解,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次社会实践活动中,某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量![]() (单位:千克)与时间
(单位:千克)与时间![]() (单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
(单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
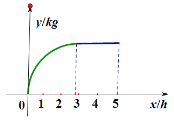
A.在前三小时内,每小时的产量逐步增加
B.在前三小时内,每小时的产量逐步减少
C.最后一小时内的产量与第三小时内的产量相同
D.最后两小时内,该车间没有生产该产品
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com