
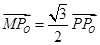 .
.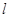 :y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.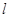 过定点(Q点除外),并求出该定点的坐标.
过定点(Q点除外),并求出该定点的坐标.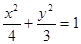 .(Ⅱ)(i)
.(Ⅱ)(i)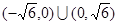 .(ii)直线过定点
.(ii)直线过定点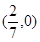 .
. 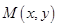 ,
,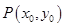 ,则由题意知
,则由题意知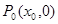 .
.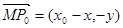 ,
,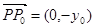 ,且
,且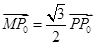 ,
,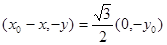 .
.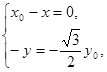 于是
于是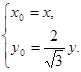
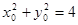 ,所以
,所以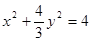 .
.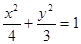 .……………………(3分)
.……………………(3分)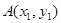 ,
,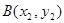 .
.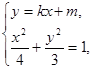
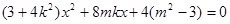 .
. 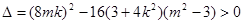 ,即
,即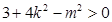 . ①
. ① ………………………………(5分)
………………………………(5分)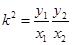 ,即
,即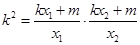 .
.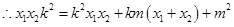 .
.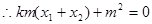 ,即
,即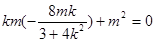 .
.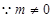 ,
,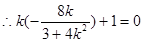 ,解得
,解得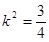 .
.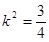 代入①,得
代入①,得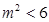 .
.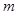 的取值范围是
的取值范围是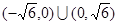 . ……………………(8分)
. ……………………(8分)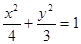 与
与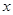 轴正半轴的交点为
轴正半轴的交点为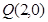 .
.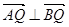 , 即
, 即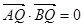 .
.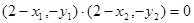 .
.
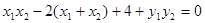 ,即
,即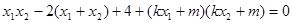 ,
,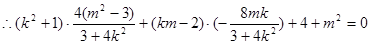 .
.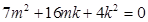 .
.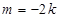 或
或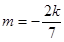 ,且均满足
,且均满足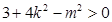 .
.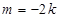 时,直线
时,直线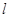 的方程为
的方程为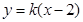 ,直线过定点
,直线过定点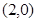 (舍去);
(舍去);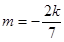 时,直线
时,直线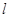 的方程为
的方程为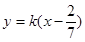 ,直线过定点
,直线过定点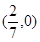 .
.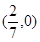 . ………………………………(13分)
. ………………………………(13分)

科目:高中数学 来源:不详 题型:解答题
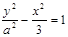 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。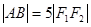 ,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

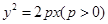 ,过其焦点F的直线交抛物线于
,过其焦点F的直线交抛物线于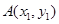 、
、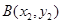 两点。过
两点。过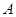 、
、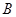 作准线的垂线,垂足分别为
作准线的垂线,垂足分别为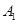 、
、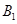 .
.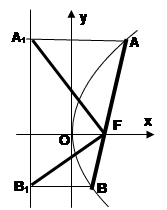
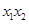 和
和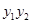 都是定值,并求出这个定值;
都是定值,并求出这个定值;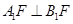 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
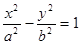 的离心率
的离心率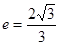 ,过
,过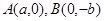 的直线到原点的距离是
的直线到原点的距离是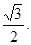
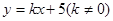 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com