
分析 (I)设切点为(a,alna-a),则切线方程为y-alna+a=lna(x-a),即y=xlna-a,利用曲线y=f(x)与直线y=x+b相切,求b的值;
(II)令面积密度为k,则k=$\frac{{∫}_{a}^{b}|lnx-lnu|dx}{b-a}$,分类讨论,求积分,即可得出结论;
(III)利用极限的思想,即可证明结论.
解答 (I)解:∵f(x)=x1nx-x,
∴f′(x)=lnx,
设切点为(a,alna-a),则切线方程为y-alna+a=lna(x-a),即y=xlna-a,
∵曲线y=f(x)与直线y=x+b相切,
∴lna=1,b=-a,
∴a=e,b=-e;
(II)解:令面积密度为k,则k=$\frac{{∫}_{a}^{b}|lnx-lnu|dx}{b-a}$,
μ≥b,k=$\frac{(xlnμ+x-xlnx){|}_{a}^{b}}{b-a}$=$\frac{(b-a)+(b-a)lnμ+alna-blnb}{b-a}$≥1+$\frac{alna-alnb}{b-a}$(μ=b时取等号)
∴kmin=1+$\frac{alna-alnb}{b-a}$
μ∈(a,b)=$\frac{{∫}_{a}^{μ}(lnμ-lnx)dx+{∫}_{μ}^{b}(lnx-lnμ)dx}{b-a}$=$\frac{alna+blnb-(a+b)+2μ-(a+b)lnμ}{b-a}$,
设g(μ)=2μ-(a+b)lnμ,g′(μ)=$\frac{2μ-(a+b)}{μ}$,
在μ∈(a,$\frac{a+b}{2}$)上g′(μ)<0,在($\frac{a+b}{2}$,b)上,g′(μ)>0,
∴g(μ)≥g($\frac{a+b}{2}$)=$\frac{alna+blnb-(a+b)ln\frac{a+b}{2}}{b-a}$,
∴kmin=$\frac{alna+blnb-(a+b)ln\frac{a+b}{2}}{b-a}$
μ∈(0,a],k=$\frac{{∫}_{a}^{b}(lnx-lnμ)dx}{b-a}$=-1-lnμ+$\frac{blnb+alna}{b-a}$≥-1+$\frac{blnb-blna}{b-a}$(μ=a时取等号),
∴kmin=-1+$\frac{blnb-blna}{b-a}$;
(III)取第二段考虑,设t=$\frac{b}{a}$(t∈(1,+∞)),g(t)=$\frac{ln\frac{2}{t+1}+tln\frac{2t}{t+1}}{t-1}$,
g′(t)=-$\frac{1}{(t-1)^{2}}$ln$\frac{4t}{(t+1)^{2}}$>0,
∴g(t)在(1,+∞)上单调递增,∵$\underset{lim}{t→1}g(t)$=$\underset{lim}{t→1}\frac{2t}{t+1}$=0,$\underset{lim}{t→∞}g(t)=\underset{lim}{t→∞}ln\frac{2}{1+\frac{1}{t}}$=ln2,
∴g(t)<ln2,
∴φ(a,b)<ln2.
点评 本题考查导数知识的运用,考查导数的几何意义,考查定积分知识,考查学生分析解决问题的能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
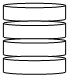 小明有4枚完全相同的硬币,每个硬币都分正反两面.他把4枚硬币叠成一摞(如图),则所有相邻两枚硬币中至少有一组同一面不相对的概率是$\frac{7}{8}$.
小明有4枚完全相同的硬币,每个硬币都分正反两面.他把4枚硬币叠成一摞(如图),则所有相邻两枚硬币中至少有一组同一面不相对的概率是$\frac{7}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD内接于抛物线x2=y,点C(3,9),AC平行于x轴,BD平行于该抛物线在点C处的切线,∠BAD=90°.
如图,已知四边形ABCD内接于抛物线x2=y,点C(3,9),AC平行于x轴,BD平行于该抛物线在点C处的切线,∠BAD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com