
���� ��I������C1����=2cos�ȣ�����2=2��cos�ȣ����û�����ʽ�ɵ�ֱ�����귽�̣����� ${C_2}����{sin^2}��=4cos��$����2sin2��=4��cos�ȣ����û�����ʽ�ɵ�ֱ�DZ����̣�
��II�����ĵ���C�ϵ�����˳��ΪP��Q��R��S��������ֱ�Ϊt1��t2��t3��t4������C�IJ������̴��������߷��̿ɵã�3t2-8t-32=0����1��0���ɵ�t1+t4������C�IJ������̴���Բ�ķ��̿ɵã�t2+t=0����2��0���ɵ�t2+t3����||PQ|-|RS||=|��t2-t1��-��t4-t3��|=|��t2+t3��-��t1+t4��|���ɵó���
��� �⣺��I������C1����=2cos�ȣ�����2=2��cos�ȣ���Ϊֱ�����귽�̣�x2+y2=2x��
���� ${C_2}����{sin^2}��=4cos��$����2sin2��=4��cos�ȣ���Ϊֱ�DZ����̣�y2=4x��
��II�����ĵ���C�ϵ�����˳��ΪP��Q��R��S��������ֱ�Ϊt1��t2��t3��t4��
����C�IJ�������Ϊ$\left\{\begin{array}{l}x=2+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$��tΪ���������������߷��̿ɵã�3t2-8t-32=0����1��0���ɵ�t1+t4=$\frac{8}{3}$��
����C�IJ�������Ϊ$\left\{\begin{array}{l}x=2+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$��tΪ����������Բ�ķ��̿ɵã�t2+t=0����2��0���ɵ�t2+t3=-1��
��||PQ|-|RS||=|��t2-t1��-��t4-t3��|=|��t2+t3��-��t1+t4��|=$|1+\frac{8}{3}|$=$\frac{11}{3}$��
���� ���⿼����ֱ�ߵIJ������̼���Ӧ�á�Բ�ļ����귽�̻�Ϊֱ�����귽�̣�������������������������������е��⣮


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 28�� | B�� | 21�� | C�� | 35�� | D�� | 56�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
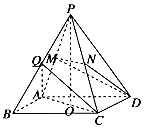 ��ͼ��������P-ABCD���ⳤ��Ϊ2����O��M��N��Q�ֱ���AC��PA��PC��PB���е㣮
��ͼ��������P-ABCD���ⳤ��Ϊ2����O��M��N��Q�ֱ���AC��PA��PC��PB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | d��b��a��c | B�� | d��a��b��c | C�� | b��c��d��a | D�� | b��d��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 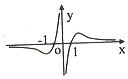 | B�� | 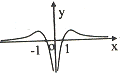 | C�� | 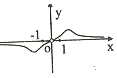 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{��}{4}$��0�� | B�� | ��$\frac{��}{8}$��0�� | C�� | ��$\frac{��}{2}$��0�� | D�� | ��$\frac{5��}{24}$��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com