练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在直三棱柱中，，且，点M在棱上，点N是BC的中点，且满足.

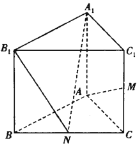
    （1）证明：平面；

    （2）若M为的中点，求二面角的正弦值.

    【答案】（1）详见解析；（2）.

    【解析】

    （1）推导出平面，从而，由，得，再由，能证明平面．
    （2）以A为原点，分别以AB、AC、为x轴、y轴、z轴建立空间直角坐标系，利用向量法能求出二面角的正弦值．

    解：（1）∵三棱柱为直三棱柱，∴

    ∵，平面，平面，且，

    ∴平面，（或者由面面垂直的性质证明）

    又∵平面，∴

    ∵，∴，

    ∵，平面，平面，且，

    ∴平面

    （2）以A为原点，分别以AB、AC、为x轴、y轴、z轴建立空间直角坐标系﹐

    设，则，，，，，，，

    ∵，∴，∴

    ∴，，

    设平面法向量为

    ，

    ∴，∴可取

    设平面法向量为

    ，

    ∴，∴可取

    ∴

    所以二面角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知是正三角形，EA，CD都垂直于平面ABC，且，二面角的平面角大小为，F是BE的中点，求证：

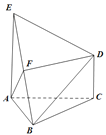
    （1）平面ABC；

    （2）平面EDB；

    （3）求几何体的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线的右顶点为A，以A为圆心，b为半径做圆，圆A与双曲线C的一条渐近线相交于M，N两点，若（为坐标原点），则双曲线C的离心率为___________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若恒成立，求实数的最大值；

    （2）在（1）成立的条件下，正实数，满足，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某网店经营的一种商品进行进价是每件10元，根据一周的销售数据得出周销售量（件）与单价（元）之间的关系如下图所示，该网店与这种商品有关的周开支均为25元.

    （1）根据周销售量图写出（件）与单价（元）之间的函数关系式；

    （2）写出利润（元）与单价（元）之间的函数关系式；当该商品的销售价格为多少元时，周利润最大？并求出最大周利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，底面是等腰梯形，，点为的中点，以为边作正方形，且平面平面.

    （1）证明：平面平面.

    （2）求二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，（，）．

    （1）若，求的极值和单调区间；

    （2）若在区间上至少存在一点，使得成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设等差数列{an}的前n项和为Sn，若S9=81，a3+a5=14．

    （1）求数列{an}的通项公式；

    （2）设bn=，若{bn}的前n项和为Tn，证明：Tn＜．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数.

    （Ⅰ）若，解不等式；

    （Ⅱ）当时，函数的最小值为，求实数的值.

    查看答案和解析>>

    同步练习册答案