
����Ŀ�������̾���ij��ũ��Ʒ����һ�����ۼ����ڣ�ÿ�۳�1t�ò�Ʒ������500Ԫ��δ�۳��IJ�Ʒ��ÿ1t����300Ԫ��������ʷ���ϣ��õ����ۼ������г���������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��������Ϊ��һ�����ۼ��ȹ�����130t��ũ��Ʒ����X����λ��t��100��X��150����ʾ��һ�����ۼ����ڵ��г���������T����λ��Ԫ����ʾ��һ�����ۼ����ھ�����ũ��Ʒ������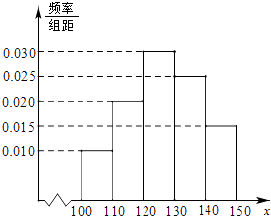
����T��ʾΪX�ĺ�����
������ֱ��ͼ��������T������57000Ԫ�ĸ��ʣ�
���𰸡��⣺��I��������ã���X��[100��130��ʱ��T=500X��300��130��X��=800X��39000��
��X��[130��150]ʱ��T=500��130=65000��
��T= ![]() ��
��
��II���ɣ�I��֪������T������57000Ԫ�����ҽ���120��X��150��
��ֱ��ͼ֪������X��[120��150]��Ƶ��Ϊ0.7��
������һ�����ۼ��ȵ�����T������57000Ԫ�ĸ��ʵĹ���ֵΪ0.7��
����������1���������⣬�ֱ�д����X��[100��130��ʱ����X��[130��150]ʱT��X�Ĺ�ϵʽ����2���ɣ�I��֪������T������57000Ԫ�����ҽ���120��X��150�����Ƶ��ֱ��ͼ���ɵó���һ�����ۼ��ȵ�����T������57000Ԫ�ĸ��ʵĹ���ֵΪ0.7��
�����㾫����������Ŀ����֪����������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������˵����ȷ���ǣ� ��
�ٺ���f��x���Ķ�������R����x��R��f��x+1����f��x�����ǡ�����f��x��Ϊ���������ij�Ҫ������
�����⡰ ![]() ���ķ��ǡ�
���ķ��ǡ� ![]() ����
����
�����⡰��x=2����x2��3x+2=0������������������⣻
��p���ڡ�ABC�У���cos2A=cos2B����A=B��q��y=sinx�ڵ�һ����������������p��qΪ�����⣮
A.�٢ڢۢ�
B.�ڢ�
C.�ۢ�
D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������S��ABCD�ĵ���ABCD�������Σ������ⳤ�����ı߳�����ȣ�MΪSA���е㣬��ֱ��BM��SC���ɵĽǵ�����ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() �����ڻ�����ͬ���ĸ�ʵ��0��a��b��c��d����f��a����f��b����f��c����f��d������ab��c��2d��ȡֵ��Χ�ǣ� ��
�����ڻ�����ͬ���ĸ�ʵ��0��a��b��c��d����f��a����f��b����f��c����f��d������ab��c��2d��ȡֵ��Χ�ǣ� ��
A.�� ![]() ��
�� ![]() ��
��
B.�� ![]() ��15��
��15��
C.[ ![]() ��15]
��15]
D.�� ![]() ��15��
��15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪aΪ����������f��x��=x��lnx��2ax����������ֵ�㣬��a��ȡֵ��ΧΪ��������
A.�����ޣ�1��
B.![]()
C.��0��1��
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ִ����ͼ�ij����ͼ�������������������һ�����ǣ�x����12������x��ֵΪ��������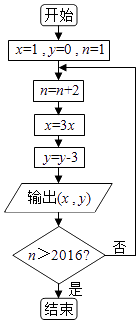
A.27
B.81
C.243
D.729
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��x2��x��1��ex ��
��1������f��x���ĵ������䣮
��2��������a�� ![]() +1��+ex=ex�ڣ�0��1�����н⣬��ʵ��a��ȡֵ��Χ��
+1��+ex=ex�ڣ�0��1�����н⣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() Ϊ�溯����
Ϊ�溯����
��1����a��ֵ��
��2���жϺ���f��x���ĵ����ԣ������ݺ��������ԵĶ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ǻ���f��x��=lg��1��ax2���Ķ�����ֵ��ֱ�Ϊ����A��B��
��1����a=1ʱ����A��B��
��2������x��A���ǡ�x��B���ı�Ҫ�������������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com