
【题目】已知P,A,B,C是半径为2的球面上的点,PA=PB=PC=2,![]() ,点B在AC上的射影为D,则三棱锥
,点B在AC上的射影为D,则三棱锥![]() 体积的最大值为( )
体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线与椭圆
,斜率为1的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且与直线
且与直线![]() 平行的直线与椭圆
平行的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
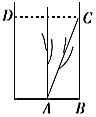
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有一个“引葭赴岸”问题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思为“今有水池1丈见方(即![]() 尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设
尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设![]() ,现有下述四个结论:
,现有下述四个结论:
①水深为12尺;②芦苇长为15尺;③![]() ;④
;④![]() .
.
其中所有正确结论的编号是( )
A.①③B.①③④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为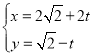 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)把曲线![]() 向下平移
向下平移![]() 个单位,然后各点横坐标变为原来的
个单位,然后各点横坐标变为原来的![]() 倍得到曲线
倍得到曲线![]() (纵坐标不变),设点
(纵坐标不变),设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为 ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与曲线
与曲线![]() 两交点所在直线的极坐标方程;
两交点所在直线的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,离心率
,离心率![]() ,
,![]() 是椭圆的左顶点,
是椭圆的左顶点,![]() 是椭圆的左焦点,
是椭圆的左焦点,![]() ,直线
,直线![]() :
:![]() .
.
(1)求椭圆![]() 方程;
方程;
(2)直线![]() 过点
过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 分别与直线
分别与直线![]() 交于
交于![]() 、
、![]() 两点,试问:以
两点,试问:以![]() 为直径的圆是否过定点,如果是,请求出定点坐标;如果不是,请说明理由.
为直径的圆是否过定点,如果是,请求出定点坐标;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com