练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    三棱锥V－ABC的中截面是△A1B1C1，则三棱锥V－A1B1C1与三棱锥A－A1BC的体积之比是

    [　　]

    A．1∶2

    B．1∶4

    C．1∶6

    D．1∶8

    答案：B
    解析：

    中截面将三棱锥的高分成相等的两部分，所以截面与原底面的面积之比为1∶4，将三棱锥A－A1BC更换为三棱锥A1－ABC，这样三棱锥V－A1B1C1与三棱锥A1－ABC的高相等，底面积之比为1∶4，于是其体积之比为1∶4．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：单元双测　同步达标活页试卷　高二数学(下A) 人教版 题型：022

    正三棱锥V－ABC中，AB＝1，侧棱VA、VB、VC两两垂直，则底面中心到侧面的距离为________

    查看答案和解析>>

    科目：高中数学 来源：甘肃省张掖市2012届高三4月高考诊断测试数学理科试题 题型：013

    已知三棱锥V－ABC中，VA＝3，VB＝4，VC＝，点E为侧棱VC上的一点，VA⊥BE，且顶点V在底面ABC上的射影为底面的垂心．如果球O是三棱锥V－ABC的外接球，则V，A两点的球面距离是

    [　　]

    A．2π

    B．

    C．π

    D．

    查看答案和解析>>

    科目：高中数学 来源：2013届北京四中高二上学期期末测试文科数学 题型：解答题

    如图，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP＝AB，BP＝BC＝2，E，F分别是PB，PC的中点。

           （1）证明：EF∥平面PAD；

           （2）求三棱锥E－ABC的体积V。

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：北京四中11-12学年高二上学期期末测试（数学文） 题型：解答题

     如图，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP＝AB，BP＝BC＝2，E，F分别是PB，PC的中点。

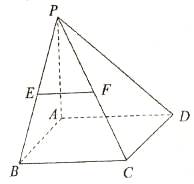
        （1）证明：EF∥平面PAD；

        （2）求三棱锥E－ABC的体积V。

     

     

     

     

    查看答案和解析>>

    同步练习册答案