
【题目】用数字![]() 组成没有重复数字的四位数.
组成没有重复数字的四位数.
(Ⅰ)可组成多少个不同的四位数?
(Ⅱ)可组成多少个不同的四位偶数?
(Ⅲ)将(Ⅰ)中的四位数按从小到大的顺序排成一数列,问第![]() 项是什么?
项是什么?
【答案】(Ⅰ)300;(Ⅱ)156;(Ⅲ)2301
【解析】
试题分析:(Ⅰ)根据排列性质,先排最高为千位,不能排0,所以可以从1,2,3,4,5中任意取一个排在最高位,有![]() 种排法,然后排剩余的三个位置,可以从0和剩余的4个数字这5个数字中,任意取3个排在剩余的3个位置,共有
种排法,然后排剩余的三个位置,可以从0和剩余的4个数字这5个数字中,任意取3个排在剩余的3个位置,共有![]() 种排法,根据乘法原理,完成这件事共有:
种排法,根据乘法原理,完成这件事共有:![]() 种;(Ⅱ)组成4位偶数,末位只能排0或2或4,末位排0时,其他位置任意排,有
种;(Ⅱ)组成4位偶数,末位只能排0或2或4,末位排0时,其他位置任意排,有![]() 种排法,末位排2或4时,最高位不能排0,此时有
种排法,末位排2或4时,最高位不能排0,此时有![]() 种,再根据加法原理,完成这件事共有
种,再根据加法原理,完成这件事共有![]() +
+![]() 种方法;(Ⅲ)将(Ⅰ)中的数从小到大排列,最高位为1时,有
种方法;(Ⅲ)将(Ⅰ)中的数从小到大排列,最高位为1时,有![]() 个,同理最高位为2时也有
个,同理最高位为2时也有![]() 个,第85个数应该是首位为2的时候,前两个数字为20时,有
个,第85个数应该是首位为2的时候,前两个数字为20时,有![]() 个,前两个数字为21时,有
个,前两个数字为21时,有![]() 个,此时共84个数,所以第85个数为2301.
个,此时共84个数,所以第85个数为2301.
试题解析:(Ⅰ)共![]() 个
个
(Ⅱ)分为两类:0在末位,则有![]() 个:0不在末位,则有
个:0不在末位,则有![]() 个.∴共60+96=156个.
个.∴共60+96=156个.
(Ⅲ)首位为1的有60个;前两位为20的有12个;
前两位为21的有12个;
因而第85项是前两位为23的最小数,即为2301


科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆:(x﹣a)2+(y﹣b)2=8(a,b为正整数)过点A(0,1),且与直线y﹣3﹣2 ![]() =0相切.
=0相切.
(1)求圆C的方程;
(2)若过点M(4,﹣1)的直线l与圆C相交于E,F两点,且 ![]() =0.求直线l的方程.
=0.求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
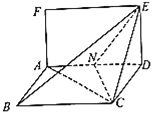
【题目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如图,其中
所在平面互相垂直,如图,其中![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,请证明
?若存在,请证明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A、B、C三点满足 ![]() =
= ![]() +
+ ![]()
![]() .
.
(1)求证:A、B、C三点共线;
(2)求 ![]() 的值;
的值;
(3)已知A(1,cosx)、B(1+cosx,cosx),x∈[0, ![]() ],f(x)=
],f(x)= ![]()
![]() ﹣(2m+
﹣(2m+ ![]() )|
)| ![]() |的最小值为﹣
|的最小值为﹣ ![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.
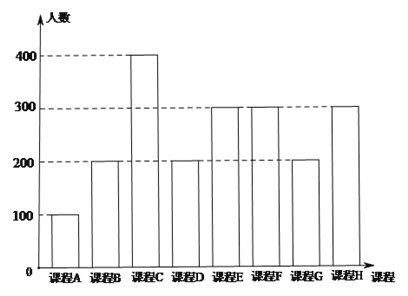
图中,课程![]() 为人文类课程,课程
为人文类课程,课程![]() 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组![]() ”).
”).
(Ⅰ)在“组![]() ”中,选择人文类课程和自然科学类课程的人数各有多少?
”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组![]() ”中选择
”中选择![]() 课
课
程或![]() 课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择
课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择![]() 课程的学生中有
课程的学生中有![]() 人参加科学营活动,每人需缴纳
人参加科学营活动,每人需缴纳![]() 元,选择
元,选择![]() 课程的学生中有
课程的学生中有![]() 人参加该活动,每人需缴纳
人参加该活动,每人需缴纳![]() 元.记选择
元.记选择![]() 课程和
课程和![]() 课程的学生自愿报名人数的情况为
课程的学生自愿报名人数的情况为![]() ,参加活动的学生缴纳费用总和为
,参加活动的学生缴纳费用总和为![]() 元.
元.
①当![]() 时,写出
时,写出![]() 的所有可能取值;
的所有可能取值;
②若选择![]() 课程的同学都参加科学营活动,求
课程的同学都参加科学营活动,求![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com