
【题目】已知![]() ,
, ![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求动点![]() 的轨迹方程,并说明轨迹
的轨迹方程,并说明轨迹![]() 是什么图形;
是什么图形;
(2)求动点![]() 与定点
与定点![]() 连线的斜率的最小值;
连线的斜率的最小值;
(3)设直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,是否存在以线段
两点,是否存在以线段![]() 为直径的圆经过
为直径的圆经过![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
平面直角坐标系中,直线![]() 的参数方程为
的参数方程为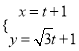 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)将分别于2017年3月5日和3月3日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与者中随机选出200人,并将这200人按年龄分组:第
.现从参与者中随机选出200人,并将这200人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
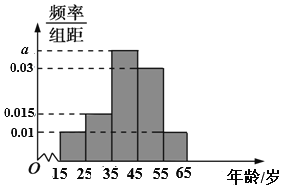
(1)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取12人,再从这12人中随机抽取3人赠送礼品,求抽取的3人中至少有![]() 人年龄在第3组的概率;
人年龄在第3组的概率;
(2)若从所有参与调查的人(人数很多)中任意选出3人,记关注民生问题的人数为X,求X的分布列与期望;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中不关注民生问题的人中老年人有10人,问是否有![]() 的把握认为是否关注民生问题与年龄有关?
的把握认为是否关注民生问题与年龄有关?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
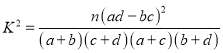 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x<﹣2或3<x≤4},B={x|x2﹣2x﹣15≤0}.求:
(1)UA;
(2)A∪B;
(3)若C={x|x>a},且B∩C=B,求a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)= ![]() 的定义域为[﹣a﹣2,b]
的定义域为[﹣a﹣2,b]
(1)求实数a,b的值;
(2)判断函数f(x)的单调性,并用定义给出证明;
(3)若实数m满足f(m﹣1)<f(1﹣2m),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() 的左,右焦点.
的左,右焦点.
(1)当![]() 时,若
时,若![]() 是椭圆
是椭圆![]() 上在第一象限内的一点,且
上在第一象限内的一点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)当椭圆![]() 的焦点在
的焦点在![]() 轴上且焦距为2时,若直线
轴上且焦距为2时,若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
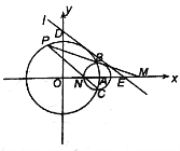
【题目】在平面直角坐标系中,圆![]() :
: ![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,以
,以![]() 为圆心的圆
为圆心的圆![]() :
: ![]() (
(![]() )与圆
)与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于
切于第一象限,且与坐标轴交于![]() ,
, ![]() ,当直线
,当直线![]() 长最小时,求直线
长最小时,求直线![]() 的方程;
的方程;
(2)设![]() 是圆
是圆![]() 上异于
上异于![]() ,
, ![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com