
分析 (Ⅰ)求出圆心坐标,和圆的标准方程,即可求圆C的极坐标方程;
(Ⅱ)分别求出直线的标准方程,利用直线和圆的位置关系即可求直线l被圆C所截得的弦长.
解答 解:(Ⅰ)∵圆C的圆心是$C(\sqrt{2},\frac{π}{4})$,
∴x=ρcosθ=$\sqrt{2}×\frac{\sqrt{2}}{2}$=1,y=ρsinθ=$\sqrt{2}×\frac{\sqrt{2}}{2}$=1,
即圆心坐标为(1,1),
则圆的标准方程为(x-1)2+(y-1)2=2,x2-2x+y2-2y=0
圆C的极坐标方程为:$ρ=2\sqrt{2}cos(θ-\frac{π}{4})$;
(Ⅱ)∵直线l的极坐标方程为$ρsin(θ+\frac{π}{4})=1+\sqrt{2}$,
∴$\frac{\sqrt{2}}{2}$ρsinθ+$\frac{\sqrt{2}}{2}$ρcosθ=1+$\sqrt{2}$,
即$x+y=2+\sqrt{2}$,
圆心到直线距离为$d=\frac{{|1+1-2-\sqrt{2}|}}{{\sqrt{2}}}=1$,圆半径为$\sqrt{2}$.
故弦长为$2\sqrt{{r^2}-{d^2}}=2$.
点评 本题主要考查参数方程和极坐标方程的应用,利用极坐标和直角坐标系之间的关系是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 0<a<$\frac{\sqrt{3}}{3}$ | B. | 0<a<$\frac{\sqrt{6}}{6}$ | C. | 1<a<$\sqrt{3}$ | D. | 1<a<$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 13(lg2)2 | C. | 10 | D. | 10(lg2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
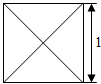 已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )| A. | 2 | B. | 3 | C. | $1+\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
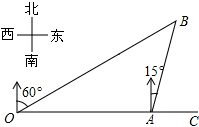
| A. | 4km | B. | 2$\sqrt{3}$km | C. | 2$\sqrt{2}$km | D. | ($\sqrt{3}$+1)km |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | 2或-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com