
已知 =(2asin2x,a),
=(2asin2x,a),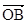 =(-1,2
=(-1,2 sinxcosx+1),O为坐标原点,a≠0,设f(x)=
sinxcosx+1),O为坐标原点,a≠0,设f(x)= ·
· +b,b>a。
+b,b>a。
(1)若a>0,写出函数y=f(x)的单调递增区间;
(2)若函数y=f(x)的定义域为[ ,π],值域为[2,5],求实数a与b的值。
,π],值域为[2,5],求实数a与b的值。
科目:高中数学 来源: 题型:
| OA |
| OB |
| 3 |
| OA |
| OB |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
在△OAB的边OA,OB上分别有一点P,Q,已知![]() :
:![]() =1:2,
=1:2, ![]() :
:![]() =3:2,连结AQ,BP,设它们交于点R,若
=3:2,连结AQ,BP,设它们交于点R,若![]() =a,
=a,![]() =b.
=b.
(1)用a与 b表示![]() ;
;
(2)过R作RH⊥AB,垂足为H,若| a|=1, | b|=2, a与 b的夹角![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一暑假作业(六)必修4数学试卷(解析版) 题型:选择题
已知| |=1,|
|=1,| |=
|= ,
, ·
· =0,点C在∠AOB内,且∠AOC=30°.设
=0,点C在∠AOB内,且∠AOC=30°.设 =m
=m +n
+n (m、n∈R),则
(m、n∈R),则 等于( )
等于( )
A. B.3 C.
B.3 C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四2.3平面向量基本定理及坐标表示(一)(解析版) 题型:选择题
设a、b是不共线的两个非零向量,已知 =2a+pb,
=2a+pb, =a+b,
=a+b, =a-2b.若A、B、D三点共线,则p的值为( )
=a-2b.若A、B、D三点共线,则p的值为( )
A.1 B.2
C.-2 D.-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com