练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，A，B，C所对的边分别为a，b，c，已知sinC= ．
    （1）若a+b=5，求△ABC面积的最大值；
    （2）若a=2，2sin2A+sinAsinC=sin2C，求b及c的长．

    【答案】
    （1）解：∵a+b=5，

    ∴ab≤（ ）2= ．

    ∴S△ABC= sinC=≤ =


    （2）解：∵2sin2A+sinAsinC=sin2C，

    ∴2a2+ac=c2．即8+2c=c2，

    解得c=4．

    由正弦定理得 ，即 ，

    解得sinA= ．∴cosA= ．

    由余弦定理得cosA= = ．即 ．

    解得b= 或2


    【解析】（1）利用基本不等式得出ab的最大值，得出面积的最大值；（2）利用正弦定理得出a，c的关系，列方程解出c，使用正弦定理解得sinA，利用余弦定理解出b．
    【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义，需要了解正弦定理:；余弦定理:;;才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn ， 已知S2=6，an+1=4Sn+1，n∈N* ．
    （1）求通项an；
    （2）设bn=an﹣n﹣4，求数列{|bn|}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某圆柱的高为2，底面周长为16，其三视图如图所示，圆柱表面上的点在正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上，从到的路径中，最短路径的长度为（ ）

    A. B. C. D. 2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PA⊥AD，AB∥CD，CD⊥AD，AD=CD=2AB=2，E，F分别为PC，CD的中点，DE=EC．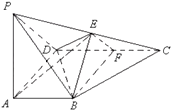

    （1）求证：平面ABE⊥平面BEF；
    （2）设PA=a，若平面EBD与平面ABCD所成锐二面角 ，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=Asin（ωx+φ）满足：f（ +x）=﹣f（ ﹣x），且f（ +x）=f（ ﹣x），则ω的一个可能取值是（ ）
    A.2
    B.3
    C.4
    D.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知公差不为0的等差数列{an}中，a1=2，且a2+1，a4+1，a8+1成等比数列．
    （1）求数列{an}通项公式；
    （2）设数列{bn}满足bn= ，求适合方程b1b2+b2b3+…+bnbn+1= 的正整数n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=Asin（ωx+ ）（ω＞0）的图象与x轴的交点的横坐标构成一个公差为 的等差数列，要得到函数g（x）=Asinωx的图象，只需将f（x）的图象（ ）
    A.向左平移 个单位
    B.向右平移 个单位
    C.向左平移 个单位
    D.向右平移 个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（cos ，﹣1）， =（ sin ，cos2 ），设函数f（x）= +1．
    （1）若x∈[0， ]，f（x）= ，求cosx的值；
    （2）在△ABC中，角A，B，C的对边分别是a，b，c，且满足2bcosA≤2c﹣ a，求f（B）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱锥的侧面是等腰直角三角形，，，，且．

    （1）求证：平面平面；

    （2）求二面角的余弦值．

    查看答案和解析>>

    同步练习册答案