
【题目】已知数列{an}满足a1=﹣1,|an﹣an﹣1|=2n﹣1(n∈N,n≥2),且{a2n﹣1}是递减数列,{a2n}是递增数列,则a2016= .
【答案】![]()
【解析】解:由|an﹣an﹣1|=2n﹣1 , (n∈N,n≥2),
则|a2n﹣a2n﹣1|=22n﹣1 , |a2n+2﹣a2n+1|=22n+1 ,
∵数列{a2n﹣1}是递减数列,且{a2n}是递增数列,
∴a2n﹣a2n﹣1<a2n+2﹣a2n+1 ,
又∵|a2n﹣a2n﹣1|=22n﹣1<|a2n+2﹣a2n+1|=22n+1 ,
∴a2n﹣a2n﹣1>0,即a2n﹣a2n﹣1=22n﹣1 ,
同理可得:a2n+3﹣a2n+2<a2n+1﹣a2n ,
又|a2n+3﹣a2n+2|>|a2n+1﹣a2n|,
则a2n+1﹣a2n=﹣22n ,
当数列{an}的项数为偶数时,令n=2k(k∈N*),
∴a2﹣a1=2,a3﹣a2=﹣22 , a4﹣a3=23 , a5﹣a4=﹣24 , …,a2015﹣a2014=﹣22014 , a2016﹣a2015=22015 .
∴a2016﹣a1=2﹣22+23﹣24+…﹣22014+22015
= ![]() =
= ![]() .
.
∴a2016= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(Ⅰ)求函数![]() 及
及![]() 的解析式;
的解析式;
(Ⅱ)用函数单调性的定义证明:函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅲ)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1. 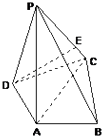
(1)求二面角A﹣PB﹣C的余弦值.
(2)在线段CP上是否存在一点E,使得DE⊥PB,若存在,求线段CE的长度,不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使| A1B1|=| A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (![]() ,2] B. [
,2] B. [![]() ,2) C. (
,2) C. (![]() ,+
,+![]() ) D. [
) D. [![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以双曲线 ![]() (a>0,b>0)上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F,且与y轴交于P、Q两点.若△MPQ为锐角三角形,则该双曲线的离心率e的范围是( )
(a>0,b>0)上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F,且与y轴交于P、Q两点.若△MPQ为锐角三角形,则该双曲线的离心率e的范围是( )
A.![]()
B.( ![]() ,
, ![]() )
)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,方程f(x)=0有3个不同的根.
,方程f(x)=0有3个不同的根.
(1)求实数m的取值范围;
(2)是否存在实数m,使得f(x)在(0,1)上恰有两个极值点x1 , x2且满足x2=2x1 , 若存在,求实数m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com