练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知向量
    i
    ，
    j
    ，
    k
    不共面，向量
    a
    =
    i
    -2
    j
    +
    k
    ，
    b
    =-
    i
    +3
    j
    +2
    k
    ，
    c
    =-3
    i
    +x
    j
    共面，则x=______．
    ∵向量
    a
    =
    i
    -2
    j
    +
    k
    ，
    b
    =-
    i
    +3
    j
    +2
    k
    ，
    c
    =-3
    i
    +x
    j
    共面
    ∴
    a
    =m
    b
    +n
    c
    ，
    ∴
    i
    -2
    j
    +
    k
    =m(-
    i
    +3
    j
    +2
    k
    )    +n(-3
    i
    +x
    j
    )
    ∴
    1+m+3n=0
    -2-3m-xn=0
    1-2m=0

    解得：x=7．
    故答案为：7．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

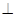    四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC底面ABCD．已知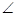ABC=45o，AB=2，BC=2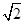，SA=SB=．

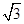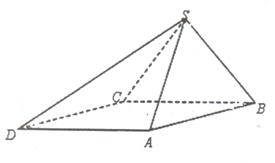
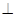    (1)证明：SABC；
    (2)求直线SD与平面SAB所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

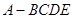    如图，四棱锥中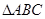，是正三角形，四边形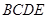是矩形，且平面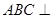平面，，．

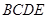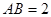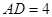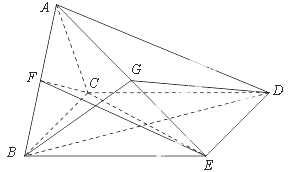
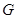    (Ⅰ)若点是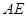的中点，求证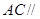：平面；
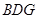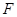    （II）试问点在线段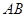上什么位置时，二面角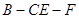的余弦值为.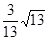

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知向量，，若∥，则锐角等于（ ）
    A．B．C．D．

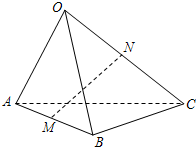
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知三棱锥O-ABC，点M，N分别为AB，OC的中点，且
    OA
    =a，
    OB
    =b，
    OC
    =c    ，用a，b，c表示
    MN
    ，则
    MN
    等于（　　）
    A．
    1
    2
    (b+c-a)    		B．
    1
    2
    (a+b-c)    		C．
    1
    2
    (a-b+c)    		D．
    1
    2
    (c-a-b)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，四面体ABCD中，点E是CD的中点，记
    AB
    =
    a
    ，
    AC
    =
    b
    ，
    AD
    =
    c
    ，则
    BE
    =（　　）
    A．
    a
    -
    1
    2
    b
    +
    1
    2
    c
    		B．-
    a
    +
    1
    2
    b
    +
    1
    2
    c
    		C．
    1
    2
    a
    -
    b
    +
    1
    2
    c
    		D．-
    1
    2
    a
    +
    b
    +
    1
    2
    c

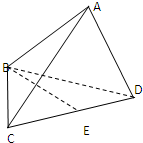
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    空间直角坐标系中，A（1，2，3），B（-2，-1，6），C（3，2，1），D（4，3，0），则直线AB与CD的位置关系是（　　）
    A．垂直B．平行
    C．异面D．相交但不垂直

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    如图，在三棱锥中，，，，，则BC和平面ACD所成角的正弦值为     ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

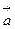    设向量的始点坐标为（3，1），终点坐标为(-1,-3),则向量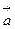的坐标为(   )
    A．(-1,-3)B．(4,4)C．(-4,-2)D．(-4,-4)

    查看答案和解析>>

    同步练习册答案