
����Ŀ����֪����f��x���Ķ�������D�������ڳ���m��M��ʹ��m��f��x����M������x��D��������ƺ���f��x����D�ϵ��н纯��������m��Ϊ����f��x�����½磬M��Ϊ����f��x�����Ͻ磻�ر�أ�����=����������m��Ϊ����f��x������ȷ�磬M��Ϊ����f��x������ȷ�磮 �����ж� ![]() �Ƿ����н纯����˵�����ɣ�
�Ƿ����н纯����˵�����ɣ�
����������f��x��=1+a2x+4x��x�ʣ����ޣ�0�������ԩ�3Ϊ�½硢3Ϊ�Ͻ���н纯������ʵ��a��ȡֵ��Χ��
���������� ![]() ��T��a����f��x������ȷ�磬��T��a����ȡֵ��Χ��
��T��a����f��x������ȷ�磬��T��a����ȡֵ��Χ��
���𰸡��⣺����f��x��= ![]() ��
�� ![]() =
= ![]() �� ��x��0����
�� ��x��0���� ![]() +
+ ![]() ��1��
��1��
��0��f��x����1������f��x�����н纯����
��t=3x �� ��t��0��
��y=t2��3t�ݩ�1��g��x����[��1��+�ޣ���
��g��x�������н纯����
���ߺ���f��x��=1+a2x+4x �� ��x�ʣ����ޣ�0�������ԩ�3Ϊ�½磬3Ϊ�Ͻ���н纯����
�ੁ3��1+a2x+4x��3�ڣ����ޣ�0���Ϻ������
����2x�� ![]() ��a��
��a�� ![]() ��2x�ڣ����ޣ�0���Ϻ������
��2x�ڣ����ޣ�0���Ϻ������
��t=2x �� g��t��=��t�� ![]() ��h��t��=��t+
��h��t��=��t+ ![]() ��
��
��x��0����0��t��1��
��t1 �� t2�ʣ�0��1������t1��t2 ��
��g��t1����g��t2��= ![]() ��0��
��0��
��g��t���ڣ�0��1��������
��g��t����g��1��=��5����a�ݩ�5��h��t1����h��t2����0��
��h��t���ڣ�0��1�����Ǽ�������
��h��t����h��1��=1��
��a��1��
���ϣ�ʵ��a�ķ�Χ��[��5��1]��
������y= ![]() ���ã�a2x=
���ã�a2x= ![]() ��
��
��x��[0��1]��a��0��
��a��a2x��2a��
��a�� ![]() ��2a��
��2a��
�� ![]() ��y��
��y�� ![]() ��
��
��T��a��= ![]() =��1+
=��1+ ![]() ��
��
��a��0��
��T��a���ķ�Χ�ǣ���1��1��
���������������н纯���Ķ���ֱ����f��x����g��x���ķ�Χ���Ӷ��ж��Ƿ��н缴�ɣ���������ת��Ϊ��2x�� ![]() ��a��
��a�� ![]() ��2x�ڣ����ޣ�0���Ϻ��������t=2x �� g��t��=��t��
��2x�ڣ����ޣ�0���Ϻ��������t=2x �� g��t��=��t�� ![]() ��h��t��=��t+
��h��t��=��t+ ![]() �����ݺ����ĵ��������t�ķ�Χ���ɣ��������a��
�����ݺ����ĵ��������t�ķ�Χ���ɣ��������a�� ![]() ��2a������
��2a������ ![]() ��y��
��y�� ![]() ���õ�T��a��=
���õ�T��a��= ![]() ���Ӷ����T��a���ķ�Χ���ɣ�
���Ӷ����T��a���ķ�Χ���ɣ�
�����㾫�������ú�������ֵ���伸���������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���ö��κ��������ʣ��䷽�������������С��ֵ������ͼ�����������С��ֵ�����ú��������Ե��жϺ��������С��ֵ��


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д� ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ������
������![]() �����ֵΪ
�����ֵΪ![]() .
.
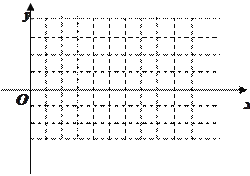
(1)��![]() �Ĵ�С��
�Ĵ�С��
(2)������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ���ٽ�����ͼ���ϸ���ĺ���������Ϊԭ����
����λ���ٽ�����ͼ���ϸ���ĺ���������Ϊԭ����![]() �������겻�䣬�õ�����
�������겻�䣬�õ�����![]() ��ͼ����������
��ͼ����������![]() ��
��![]() ��ͼ��
��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=cos2x+2 ![]() sinxcosx��sin2x��
sinxcosx��sin2x��
��1����f��x������С�����ں�ֵ��
��2���ڡ�ABC�У���A��B��C���Եı߷ֱ���a��b��c���� ![]() ��a2=bc�����жϡ�ABC����״��
��a2=bc�����жϡ�ABC����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϊ ![]() ����Բ
����Բ![]() �����ҽ���Ϊ
�����ҽ���Ϊ![]() , ��P��E��һ��,
, ��P��E��һ��, ![]() ,
, ![]() ����Բ�İ뾶Ϊ
����Բ�İ뾶Ϊ ![]() .
.
(1)��E�ķ���;
(2)����ABCD��������C��D��ֱ��![]() ����A��B����ԲE��,������ABCD���ܳ�Ϊ
����A��B����ԲE��,������ABCD���ܳ�Ϊ ![]() , ��ֱ��AB�ķ���.
, ��ֱ��AB�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
�� ![]() ������
������![]() �ϵĶ���
�ϵĶ���![]() ����
����![]() ��ֱ��
��ֱ��![]() ������
������![]() ����һ������Ϊ
����һ������Ϊ![]() ��
��
������������![]() �ı����̣�
�ı����̣�
���������![]() ����
����![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ij�豸��ʹ������x���꣩����֧����ά����y����Ԫ�������µ�ͳ�����ϣ�
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
��1������ɢ��ͼ���ж��Ƿ�������أ�
��2�����������أ������Իع鷽�̣�
��3������ʹ������Ϊ10��ʱ��ά�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2x3+bx2+cx���䵼����y=f�䣨x����ͼ����ͼ��ʾ�������㣨1��0������2��0���� ������f��x���Ľ���ʽ��
����������f��x����m=0ǡ��2��������m��ֵ��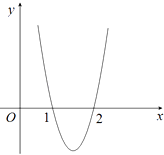
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Ox��Oy��ƽ�����ཻ��45��ǵ��������ᣬ ![]() ��
�� ![]() �ֱ���x�ᡢy��������ͬ��ĵ�λ������������
�ֱ���x�ᡢy��������ͬ��ĵ�λ������������ ![]() =x
=x ![]() +y
+y ![]() ������������ԣ�x��y����������
������������ԣ�x��y���������� ![]() ������ϵxOy�е����꣬�ڴ�����ϵ�£�����
������ϵxOy�е����꣬�ڴ�����ϵ�£����� ![]() =����2��2
=����2��2 ![]() ����
���� ![]() =��2��0����
=��2��0���� ![]() =��5����3
=��5����3 ![]() �������������ⲻ��ȷ���ǣ� ��
�������������ⲻ��ȷ���ǣ� �� 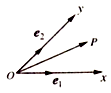
A.![]() =��1��0��
=��1��0��
B.| ![]() |=2
|=2 ![]()
C.![]() ��
�� ![]()
D.![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
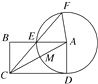
����Ŀ����ͼ���ھ���ABCD�У���AΪԲ�ģ�ADΪ�뾶��Բ��AC��AB��M��E.CE���ӳ��߽���A��F��CM��2��AB��4.
(1)���A�İ뾶��
(2)��CE�ij��͡�AFC�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com