
【题目】已知( ![]() ﹣
﹣ ![]() )n的展开式中,前三项系数的绝对值依次成等差数列.
)n的展开式中,前三项系数的绝对值依次成等差数列.
(1)证明:展开式中没有常数项;
(2)求展开式中所有有理项.
【答案】
(1)解:依题意,前三项系数的绝对值是1,C1n( ![]() ),C2n(
),C2n( ![]() )2,
)2,
且2C1n ![]() =1+C2n(
=1+C2n( ![]() )2,
)2,
即n2﹣9n+8=0,∴n=8(n=1舍去),
∴展开式的第k+1项为Ck8( ![]() )8﹣k(﹣
)8﹣k(﹣ ![]() )k
)k
=(﹣ ![]() )kCk8x
)kCk8x ![]() x﹣
x﹣ ![]() =(﹣1)kCk8x
=(﹣1)kCk8x ![]() .
.
证明:若第k+1项为常数项,
当且仅当 ![]() =0,即3k=16,
=0,即3k=16,
∵k∈Z,∴这不可能,∴展开式中没有常数项
(2)解:若第k+1项为有理项,当且仅当 ![]() 为整数,
为整数,
∵0≤k≤8,k∈Z,∴k=0,4,8,
即展开式中的有理项共有三项,它们是:
T1=x4,T5= ![]() x,T9=
x,T9= ![]() x﹣2
x﹣2
【解析】(1)利用二项展开式的通项公式求出前三项的系数,列出方程求出n,再利用二项展开式的通项公式求出通项,令x的指数为0得到常数项,方程无解,得证.(2)令展开式中的x的指数为有理数,求出k值,再求出相应的有理项.
【考点精析】掌握等差数列的性质和二项式定理的通项公式是解答本题的根本,需要知道在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列;二项式通项公式:![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( ) 
A.0
B.3 ![]()
C.6 ![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况,![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
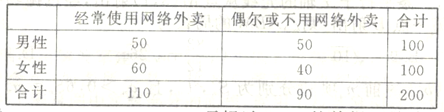
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈[ ![]() ,
, ![]() ],都有f(x)﹣2mx≤1成立,求实数m的取值范围.
],都有f(x)﹣2mx≤1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数y=sin3x的图象向右平移 ![]() 个长度单位,所得曲线的对应函数式( )
个长度单位,所得曲线的对应函数式( )
A.y=sin(3x﹣ ![]() )
)
B.y=sin(3x+ ![]() )
)
C.y=sin(3x﹣ ![]() )
)
D.y=sin(3x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式2xlnx≥﹣x2+ax﹣3对x∈(0,+∞)恒成立,则实数a的取值范围是( )
A.(﹣∞,0)
B.(0,+∞)
C.(﹣∞,4]
D.[4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 的最大值为6,求常数
的最大值为6,求常数![]() 的值;
的值;
(2)若函数![]() 有两个零点
有两个零点![]() 和
和![]() ,求
,求![]() 的取值范围,并求
的取值范围,并求![]() 和
和![]() 的值;
的值;
(3)在(1)的条件下,若![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB. 
(1)求证:平面C1CD⊥平面ABC;
(2)求证:AC1∥平面CDB1;
(3)求三棱锥D﹣CAB1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com