
【题目】已知函数![]()
(1)若函数![]() 在
在![]() 处取得极值1,证明:
处取得极值1,证明:![]()
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)求出函数![]() 的导函数
的导函数![]() ,由
,由![]() 在
在![]() 处取得极值1,可得
处取得极值1,可得![]() 且
且![]() .解出
.解出![]() ,构造函数
,构造函数![]() ,分析其单调性,结合
,分析其单调性,结合![]() ,即可得到
,即可得到![]() 的范围,命题得证;
的范围,命题得证;
(2)由![]() 分离参数,得到
分离参数,得到![]() 恒成立,构造函数
恒成立,构造函数![]() ,求导函数
,求导函数![]() ,再构造函数
,再构造函数![]() ,进行二次求导
,进行二次求导![]() .由
.由![]() 知
知![]() ,则
,则![]() 在
在![]() 上单调递增.根据零点存在定理可知
上单调递增.根据零点存在定理可知![]() 有唯一零点
有唯一零点![]() ,且
,且![]() .由此判断出
.由此判断出![]() 时,
时,![]() 单调递减,
单调递减,![]() 时,
时,![]() 单调递增,则
单调递增,则![]() ,即
,即![]() .由
.由![]() 得
得![]() ,再次构造函数
,再次构造函数![]() ,求导分析单调性,从而得
,求导分析单调性,从而得![]() ,即
,即![]() ,最终求得
,最终求得![]() ,则
,则![]() .
.
解:(1)由题知,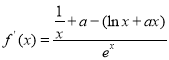
∵函数![]() 在
在![]() ,处取得极值1,
,处取得极值1,
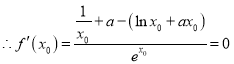 ,且
,且![]() ,
,
![]() ,
,
![]() ,
,
令![]() ,则
,则![]()
![]() 为增函数,
为增函数,
![]()
![]() ,即
,即![]() 成立.
成立.
(2)不等式![]() 恒成立,
恒成立,
即不等式![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
令![]() ,则
,则![]()
令![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
![]() 有唯一零点
有唯一零点![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增.
单调递增.
![]() ,
,
![]()
由![]() 整理得
整理得![]()
![]() ,
,![]()
令![]() ,则方程
,则方程![]() 等价于
等价于![]()
而![]() 在
在![]() 上恒大于零,
上恒大于零,
![]() 在
在![]() 上单调递增,
上单调递增,
![]() .
.
![]()
![]()
![]() ,
,
![]()
∴实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆上的一个动点(不与左、右顶点重合),且
是椭圆上的一个动点(不与左、右顶点重合),且![]() 的周长为6,点
的周长为6,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,直线
,直线![]() 交于点
交于点![]() .
.

(1)求椭圆方程;
(2)若直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
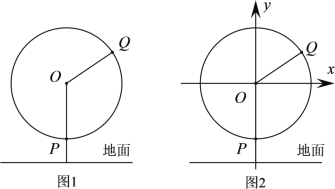
【题目】随着我国综合国力的不断增强,不少综合性娱乐场所都引进了“摩天轮”这一娱乐设施.(如图1)有一半径为40m的摩天轮,轴心![]() 距地面50m,摩天轮按逆时针方向做匀速旋转,转一周需要3min.点
距地面50m,摩天轮按逆时针方向做匀速旋转,转一周需要3min.点![]() 与点
与点![]() 都在摩天轮上,且点
都在摩天轮上,且点![]() 相对于点
相对于点![]() 落后1min,当点
落后1min,当点![]() 在摩天轮的最低点处时开始计时,以轴心
在摩天轮的最低点处时开始计时,以轴心![]() 为坐标原点,平行于地面且在摩天轮所在平面内的直线为
为坐标原点,平行于地面且在摩天轮所在平面内的直线为![]() 轴,建立图2所示的平面直角坐标系.
轴,建立图2所示的平面直角坐标系.

(1)若![]() ,求点
,求点![]() 的纵坐标关于时间
的纵坐标关于时间![]() 的函数关系式
的函数关系式![]() ;
;
(2)若![]() ,求点
,求点![]() 距离地面的高度关于时间
距离地面的高度关于时间![]() 的函数关系式
的函数关系式![]() ,并求
,并求![]() 时,点
时,点![]() 离地面的高度(结果精确到0.1,计算所用数据:
离地面的高度(结果精确到0.1,计算所用数据:![]() )
)
(3)若![]() ,当
,当![]() ,
,![]() 两点距离地面的高度差不超过
两点距离地面的高度差不超过![]() 时,求时间
时,求时间![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com