
【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点M的极坐标为 ![]() ,圆C的参数方程为
,圆C的参数方程为 ![]() (α为参数).
(α为参数).
(1)直线l过M且与圆C相切,求直线l的极坐标方程;
(2)过点P(0,m)且斜率为 ![]() 的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
【答案】
(1)解:M的直角坐标为(3,3),
圆C的直角坐标方程为(x﹣1)2+y2=4,
设直线l:y﹣3=k(x﹣3),即l:kx﹣y﹣3k+3=0,
因为直线l与圆C相切,所以 ![]() ,解得
,解得 ![]() ,
,
此时直线l的方程为5x﹣12y+21=0,
若直线l的斜率不存在时,直线l的方程为x=3,
所以直线l的极坐标方程为5ρcosθ﹣12ρsinθ+21=0或ρcosθ=3
(2)解:将直线l'的参数方程 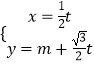 (t为参数),
(t为参数),
代入圆C的方程(x﹣1)2+y2=4,
得:t2+( ![]() m﹣1)t+m2﹣3=0,
m﹣1)t+m2﹣3=0,
![]() =
= ![]() ,
,
设PA=t1,PB=t2,则 ![]() ,
,
因为|PA||PB|=6,所以 ![]() ,
,
所以m2﹣3=±6,解得m=±3,
由△>0知,所求m的值为﹣3
【解析】(1)根据参数方程和极坐标方程和普通方程的关系进行转化即可;(2)将直线方程代入圆的方程得到关于t的二次方程,根据判别式求出关于m的方程,解出即可.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与函数
的图象与函数![]() 的图象有三个不同的交点
的图象有三个不同的交点![]() 、
、![]() 、
、![]() ,其中
,其中![]() .给出下列四个结论: ①
.给出下列四个结论: ①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中,正确结论的个数有( )个
.其中,正确结论的个数有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校的800名男生中随机抽取50名测量其身高,被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分组:第一组
之间,将测量结果按如下方式分组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4.
,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4.

(1)请补全频率分布直方图并求第七组的频率;
(2)估计该校的800名男生的身高的中位数以及身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为![]() ,
,![]() ,事件
,事件![]() ,事件
,事件![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,PA⊥平面ABCD,CD⊥AD,BC∥AD,
中,PA⊥平面ABCD,CD⊥AD,BC∥AD,![]() .
.

(Ⅰ)求证:CD⊥PD;
(Ⅱ)求证:BD⊥平面PAB;
(Ⅲ)在棱PD上是否存在点M,使CM∥平面PAB,若存在,确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从![]() 道题中(
道题中(![]() 道甲组题和
道甲组题和![]() 道乙组题)不放回地依次任取
道乙组题)不放回地依次任取![]() 道作答.
道作答.
(1)求该考生在第一次抽到甲组题的条件下,第二次和第三次均抽到乙组题的概率;
(2)规定理科考生需作答![]() 道甲组题和
道甲组题和![]() 道乙组题,该考生答对甲组题的概率均为
道乙组题,该考生答对甲组题的概率均为![]() ,答对乙组题的概率均为
,答对乙组题的概率均为![]() ,若每题答对得
,若每题答对得![]() ,否则得零分.现该生已抽到
,否则得零分.现该生已抽到![]() 道题(
道题(![]() 道甲组题和
道甲组题和![]() 道乙组题),求其所得总分的分布列与数学期望.
道乙组题),求其所得总分的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的x∈R,都有f(﹣x)+f(x)=﹣6,且当x≥0时,f(x)=2x﹣4,定义在R上的函数g(x)=a(x﹣a)(x+a+1),两函数同时满足:x∈R,都有f(x)<0或g(x)<0;x∈(﹣∞,﹣1),f(x)g(x)<0,则实数a的取值范围为( )
A.(﹣3,0)
B.![]()
C.(﹣3,﹣1)
D.(﹣3,﹣1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校参加某项竞赛仅有一个名额,结合平时训练成绩,甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:设计6道测试题,若这6道题中,甲能正确解答其中的4道,乙能正确解答每个题目的概率均为![]() .假设甲、乙两名学生解答每道测试题都相互独立,互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答.
.假设甲、乙两名学生解答每道测试题都相互独立,互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答.
(1)求甲、乙两名学生共答对2道测试题的概率;
(2)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点
=1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点 ![]() .
.
(1)求椭圆C的方程;
(2)设M,N为椭圆C上不同的两点,A,B分别为椭圆C上的左右顶点,直线MN既不平行与坐标轴,也不过椭圆C的右焦点F,若∠AFM=∠BFN,求证:直线MN过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com